题目内容
已知圆C:(x-3)2+(y-4)2=1,点A(0,-1)与B(0,1),P为圆C上动点,当|PA|2+|PB|2取最大值时点P坐标是 .
考点:圆的标准方程
专题:计算题,直线与圆
分析:设P(x,y),则d=|PA|2+|PB|2=x2+(y+1)2+x2+(y-1)2=2(x2+y2)+2,
的几何意义是P(x,y)到原点的距离,由直线y=
x与圆C:(x-3)2+(y-4)2=1,可得(5x-12)(5x-18)=0,即可求出当|PA|2+|PB|2取最大值时点P坐标.
| x2+y2 |
| 4 |
| 3 |
解答:
解:设P(x,y),则d=|PA|2+|PB|2=x2+(y+1)2+x2+(y-1)2=2(x2+y2)+2,
的几何意义是P(x,y)到原点的距离,
由已知,圆心C(3,4),半径为1,C到O的距离|CO|=5,
∴
的最大值是5+1=6,
∴d的最大值为2×62+2=74,
由直线y=
x与圆C:(x-3)2+(y-4)2=1,可得(5x-12)(5x-18)=0,
∴x=
或x=
,
∴当|PA|2+|PB|2取最大值时点P坐标是(
,
).
故答案为:(
,
).
| x2+y2 |
由已知,圆心C(3,4),半径为1,C到O的距离|CO|=5,
∴
| x2+y2 |
∴d的最大值为2×62+2=74,
由直线y=
| 4 |
| 3 |
∴x=
| 12 |
| 5 |
| 18 |
| 5 |
∴当|PA|2+|PB|2取最大值时点P坐标是(
| 18 |
| 5 |
| 24 |
| 5 |
故答案为:(
| 18 |
| 5 |
| 24 |
| 5 |
点评:本题考查圆的方程,考查直线与圆的位置关系,正确转化是关键.

练习册系列答案
相关题目
已知i是虚数单位,m和n都是实数,且m(1+i)=
+m,则(
)2015=( )
| 3 |
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
z=
(i是虚数单位)则z的共轭复数为( )
| 5i |
| 1-2i |
| A、2-i | B、2+i |
| C、-2-i | D、-2+i |
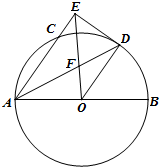 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若