题目内容
关于x的不等式(ax-1)(lnx+ax)≥0在(0,+∞)上恒成立,则实数a的取值范围是 .
考点:函数恒成立问题
专题:计算题,导数的综合应用
分析:分类讨论,将不等式转化,即可求出实数a的取值范围.
解答:
解:a<0,则lnx+ax≤0,令y=lnx+ax,则y′=
+a,
∴0<x<-
时,y′>0,x>-
时,y′<0
∴x=-
时,函数取得最大值ln(-
)-1,
∵lnx+ax≤0,
∴ln(-
)-1≤0,∴-
≤a<0;
a=0时,则lnx≤0,在(0,+∞)上不恒成立,不合题意;
a>0时,
或
,无解,
综上,-
≤a<0.
| 1 |
| x |
∴0<x<-
| 1 |
| a |
| 1 |
| a |
∴x=-
| 1 |
| a |
| 1 |
| a |
∵lnx+ax≤0,
∴ln(-
| 1 |
| a |
| 1 |
| e |
a=0时,则lnx≤0,在(0,+∞)上不恒成立,不合题意;
a>0时,
|
|
综上,-
| 1 |
| e |
点评:本题考查求实数a的取值范围,考查导数知识,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
在区间[-
,
]上随机取一个数x,则cosπx的值介于
与
之间的概率为( )
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
z=
(i是虚数单位)则z的共轭复数为( )
| 5i |
| 1-2i |
| A、2-i | B、2+i |
| C、-2-i | D、-2+i |
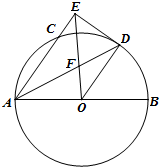 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若