题目内容
以极点为原点,以极轴为x轴正半轴建立平面直角坐标系,已知曲线C的极坐标方程为ρ=10,曲线C′的参数方程为
(α为参数).
(I)判断两曲线的位置关系;
(Ⅱ)若直线l与曲线C和C′均相切,求直线l的极坐标方程.
|
(I)判断两曲线的位置关系;
(Ⅱ)若直线l与曲线C和C′均相切,求直线l的极坐标方程.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(Ⅰ)直接利用关系式把极坐标方程转化成直角坐标方程,再进一步判断曲线的位置关系.
(Ⅱ)利用上步的结论,利用建立方程组求出切点的坐标,进一步利用点斜式求出切线的方程.
(Ⅱ)利用上步的结论,利用建立方程组求出切点的坐标,进一步利用点斜式求出切线的方程.
解答:
解:(Ⅰ)曲线C的极坐标方程为ρ=10转化成直角坐标方程为:x2+y2=100,
所以曲线C是以原点为圆心,10为半径的圆.
曲线C′的参数方程为
(α为参数)转化成直角坐标方程为:(x-3)2+(y+4)2=25.
所以曲线C′的方程表示以(3,-4)为圆心5为半径的圆.
所以两圆的圆心距等于半径之差.
则两圆相内切.
(Ⅱ)由(Ⅰ)建立方程组:
,
解得:
,
所以切点为:(6,-8),
且公切线的斜率为k=
,
则直线方程为:3x-4y-50=0,
转化成极坐标方程为:3ρcosθ-4ρsinθ-50=0.
所以曲线C是以原点为圆心,10为半径的圆.
曲线C′的参数方程为
|
所以曲线C′的方程表示以(3,-4)为圆心5为半径的圆.
所以两圆的圆心距等于半径之差.
则两圆相内切.
(Ⅱ)由(Ⅰ)建立方程组:
|
解得:
|
所以切点为:(6,-8),
且公切线的斜率为k=
| 3 |
| 4 |
则直线方程为:3x-4y-50=0,
转化成极坐标方程为:3ρcosθ-4ρsinθ-50=0.
点评:本题考查的知识要点:参数方程和极坐标方程与直角坐标方程的互化,两圆位置关系的判定,利用点斜式求直线的方程.

练习册系列答案
相关题目
若二项式(x+
)7的展开式中
的系数与
的系数之比是35:21,则a=( )
| a |
| x |
| 1 |
| x |
| 1 |
| x3 |
| A、1 | B、2 | C、-1 | D、-2 |
| ∫ | 2 -2 |
| A、2e2-2 |
| B、2e2 |
| C、e2-e-2 |
| D、e2+e-2-2 |
在区间[-
,
]上随机取一个数x,则cosπx的值介于
与
之间的概率为( )
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
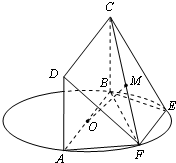 如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.
如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.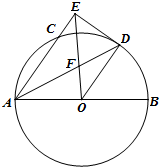 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若