题目内容
设函数fn(x)=x-
+
-…+
-ln(1+x),n∈N*.
(Ⅰ)判断函数fn(x)在(0,1)内的单调性,并说明理由;
(Ⅱ)求最大的整数α,使得|fn(x)|<
对所有的n∈N*及x∈(0,1)都成立.(注:ln2≈0.6931.)
| x2 |
| 2 |
| x3 |
| 3 |
| (-1)n+1xn |
| n |
(Ⅰ)判断函数fn(x)在(0,1)内的单调性,并说明理由;
(Ⅱ)求最大的整数α,使得|fn(x)|<
| 1 |
| nα |
考点:利用导数研究函数的单调性
专题:导数的概念及应用,导数的综合应用
分析:(1)利用导数与函数单调性的关系判断;
(2)利用(1)的结论,对n的奇偶性进行讨论并利用不等式性质进行放缩.
(2)利用(1)的结论,对n的奇偶性进行讨论并利用不等式性质进行放缩.
解答:
解:(I)函数fn(x)的导数fn′(x)=1-x+x2-…+(-1)n+1xn-1-
…(2分)
=
-
=
,…(4分)
故在(0,1)内,当n为奇数时,fn′(x)=
>0,则函数fn(x)在(0,1)内单调递增;
当n为偶数时,fn′(x)=-
<0,则函数fn(x)在(0,1)内单调递减.…(6分)
(II)注意到对任意n∈N*,fn(0)=0,…(7分)
由(I),对任意x∈(0,1),
当n为奇数时,fn(x)>0;当n为偶数时,fn(x)<0.…(8分)
故当n为奇数时,n+1为偶数,fn+1(x)=fn(x)-
<0,即fn(x)<
,
而fn(x)>0,故|fn(x)|<
; …(10分)
同理,当n为偶数时,仍有|fn(x)|<
.
所以对任意n∈N*及x∈(0,1),都有|fn(x)|<
.…(12分)
又x∈(0,1),故
<
,即|fn(x)|<
<
.
因此α=1能够使得|fn(x)|<
对所有的n∈N*及x∈(0,1)都成立.…(14分)
再注意到|f3(1)|=
-ln2>
,故当x充分接近1时,必有|f3(x)|>
,
这表明α≥2不能使得|fn(x)|<
对所有的n∈N*及x∈(0,1)都成立.
所以α=1为满足要求的最大整数.…(15分)
| 1 |
| 1+x |
=
| 1-(-1)n+1xn-1•(-x) |
| 1-(-x) |
| 1 |
| 1+x |
| (-1)n+1xn |
| 1+x |
故在(0,1)内,当n为奇数时,fn′(x)=
| xn |
| 1+x |
当n为偶数时,fn′(x)=-
| xn |
| 1+x |
(II)注意到对任意n∈N*,fn(0)=0,…(7分)
由(I),对任意x∈(0,1),
当n为奇数时,fn(x)>0;当n为偶数时,fn(x)<0.…(8分)
故当n为奇数时,n+1为偶数,fn+1(x)=fn(x)-
| xn+1 |
| n+1 |
| xn+1 |
| n+1 |
而fn(x)>0,故|fn(x)|<
| xn+1 |
| n+1 |
同理,当n为偶数时,仍有|fn(x)|<
| xn+1 |
| n+1 |
所以对任意n∈N*及x∈(0,1),都有|fn(x)|<
| xn+1 |
| n+1 |
又x∈(0,1),故
| xn+1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n |
因此α=1能够使得|fn(x)|<
| 1 |
| nα |
再注意到|f3(1)|=
| 5 |
| 6 |
| 1 |
| 32 |
| 1 |
| 32 |
这表明α≥2不能使得|fn(x)|<
| 1 |
| nα |
所以α=1为满足要求的最大整数.…(15分)
点评:考查利用导数判断函数单调性的方法以及恒成立问题的转化思想等综合运用能力,属难题.

练习册系列答案
相关题目
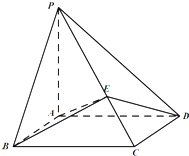 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=