题目内容

如图，由曲线y=x2+4与直线y=5x，x=0，x=4所围成平面图形的面积．
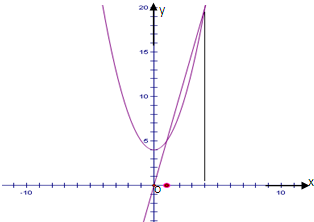
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：先求出曲线与直线的交点，设围成的平面图形面积为A，利用定积分求出A即可．
解答： 解：联立曲线y=x2+4与直线y=5x得（1，5），（4，20），
∴曲线y=x2+2与直线y=3x，x=0，x=2所围成的平面图形的面积
S=
∫
1
0
（x2+4-5x）dx+
∫
4
1
[5x-（x2+4）]dx=（
1
3
x3-
5
2
x2+4x）
|
1
0
+（
5
2
x2-
1
3
x3-4x）
|
4
1
=
19
3
．
点评：本题考查学生利用定积分求平面图形面积的能力，考查运算能力，基础题．
练习册系列答案
相关题目
在△ABC中，内角A、B、C的对边分别是a、b、c，且bsinB=asinA+（c-
3
a）sinC．
（1）求角B的大小；
（2）设b2-4bcos（A-C）+4=0，求△ABC的面积S．
已知函数f(x)=
2x-1
x+1
，x∈[1，17]．
（1）证明函数f（x）在[1，17]上为增函数；
（2）求此函数的最大值和最小值．
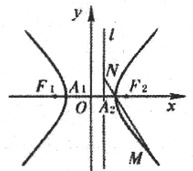如图，A1、A2、F1、F2分别是双曲线C：
x2
9
-
y2
16
=1的左、右顶点和左、右焦点，M（x0、y0）是双曲线C上任意一点，直线MA2与动直线l：x=
9
x0
相交于点N．
（1）求点N的轨迹E的方程；
（2）点B为曲线E上第一象限内的一点，连接F1B交曲线E于另一点D，记四边形A1 A2BD对角线的交点为G，证明：点G在定直线上．
设函数fn（x）=x-
x2
2
+
x3
3
-…+
(-1)n+1xn
n
-ln（1+x），n∈N*．
（Ⅰ）判断函数fn（x）在（0，1）内的单调性，并说明理由；
（Ⅱ）求最大的整数α，使得|fn（x）|＜
1
nα
对所有的n∈N*及x∈（0，1）都成立．（注：ln2≈0.6931．）
判断方程sinx+1=2cosx，x∈[0，3π]的解的个数．
如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
2
．M是AD的中点．
（1）证明：平面ABC⊥平面ADC；
（2）若∠BDC=60°，求直线BM与CD所成的余弦值的大小．
（3）若∠BDC=60°，求二面角C-BM-D的大小．
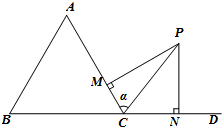设△ABC三个内角A、B、C所对的边分别为a，b，c．已知C=
π
3
，acosA=bcosB．
（1）求角A的大小；
（2）如图，在△ABC的外角∠ACD内取一点P，使得PC=2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA=α，求PM+PN的最大值及此时α的取值．
在0°～360°范围内，与1000°角终边相同的角：
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网