题目内容
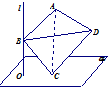 如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,
如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,(1)线段BC、AD两中点连线的长度是
(2)当O到AD的距离为最大时,正四面体在平面α上的射影面积为
考点:平行投影及平行投影作图法
专题:计算题,空间位置关系与距离
分析:(1)利用勾股定理,即可求出线段BC、AD两中点连线的长度;
(2)确定直线BC与动点O的空间关系,得到最大距离为AD到球心的距离+半径,再考虑取得最大距离时四面体的投影情况,即可求得结论.
(2)确定直线BC与动点O的空间关系,得到最大距离为AD到球心的距离+半径,再考虑取得最大距离时四面体的投影情况,即可求得结论.
解答:
解:(1)∵正四面体ABCD的棱长为4,
∴线段BC、AD两中点连线的长度是
=2
;
(2)由题意,直线BC与动点O的空间关系:点O是以BC为直径的球面上的点,所以O到AD的距离为四面体上以BC为直径的球面上的点到AD的距离,最大距离为AD到球心的距离(即BC与AD的公垂线)+半径=2
+2.
再考虑取得最大距离时四面体的投影情况,此时我们注意到AD垂直平面OBC,且平行平面α,故其投影是以AD为底,O到AD 的距离投影,即(2
+2)cos45°=2+
为高的等腰三角形,其面积=
×4×(2+
)=4+2
.
故答案为:2
,4+2
.
∴线段BC、AD两中点连线的长度是
(2
|
| 2 |
(2)由题意,直线BC与动点O的空间关系:点O是以BC为直径的球面上的点,所以O到AD的距离为四面体上以BC为直径的球面上的点到AD的距离,最大距离为AD到球心的距离(即BC与AD的公垂线)+半径=2
| 2 |
再考虑取得最大距离时四面体的投影情况,此时我们注意到AD垂直平面OBC,且平行平面α,故其投影是以AD为底,O到AD 的距离投影,即(2
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:2
| 2 |
| 2 |
点评:本题考查点、线、面间的距离计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知f(x)=
,则下列正确的是( )
| ex-e-x |
| 2 |
| A、奇函数,在R上为增函数 |
| B、偶函数,在R上为增函数 |
| C、奇函数,在R上为减函数 |
| D、偶函数,在R上为减函数 |
已知圆C:x2+y2-2x+4y-11=0,在区间[-4,6]上任取实数m,则直线l:x+y+m=0与圆C相交所得△ABC为钝角三角形(其中A、B为交点,C为圆心)的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题是真命题的是( )
| A、到两定点距离之和为常数的点的轨迹是椭圆 | ||||
B、到定直线x=
| ||||
C、到定点F(-c,0)和定直线x=-
| ||||
D、到定直线x=
|
 如图,|
如图,|