题目内容
已知集合A={x|y=
},B={x|x2+x-6<0},求(1)A∩B;(2)(CRA)∪B.
|
考点:交、并、补集的混合运算,交集及其运算
专题:集合
分析:求出A中x的范围确定出A,求出B中不等式的解集确定出B,
(1)求出A与B的交集即可;
(2)求出A补集与B并集即可.
(1)求出A与B的交集即可;
(2)求出A补集与B并集即可.
解答:
解:由A中y=
,得:
≥0,即(2x+1)(x-1)≥0,且x-1≠0,
解得:x≤-
或x>1,即A=(-∞,-
]∪(1,+∞),
由B中不等式变形得:(x-2)(x+3)<0,
解得:-3<x<2,即B=(-3,2),
(1)A∩B=(-3,-
]∪(1,2);
(2)∁RA=(-
,1],
则(∁RA)∪B=(-3,2).
|
| 2x+1 |
| x-1 |
解得:x≤-
| 1 |
| 2 |
| 1 |
| 2 |
由B中不等式变形得:(x-2)(x+3)<0,
解得:-3<x<2,即B=(-3,2),
(1)A∩B=(-3,-
| 1 |
| 2 |
(2)∁RA=(-
| 1 |
| 2 |
则(∁RA)∪B=(-3,2).
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
关于x的不等式|2x-3|+|4-2x|>a恒成立的充分不必要条件是( )
| A、0<a<1 | B、0<a≤1 |
| C、1<a<7 | D、a<1 |
复数
(i是虚数单位)在复平面内对应的点位于( )
| 25 |
| 3-4i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知U={x|-1≤x≤3},A={x|-1≤x<3},B={x|x2-2x-3=0},C={x|-1<x<3},则有( )
| A、A?C | B、C∪B=C |
| C、B∩U=C | D、C∪A=B |
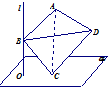 如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,
如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,