题目内容
下列命题是真命题的是( )
| A、到两定点距离之和为常数的点的轨迹是椭圆 | ||||
B、到定直线x=
| ||||
C、到定点F(-c,0)和定直线x=-
| ||||
D、到定直线x=
|
考点:椭圆的定义
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆的两个定义,对选项中的命题进行判断即可.
解答:
解:根据椭圆的定义是平面内到两定点的距离之和为定值的点的集合(该定值大于两点间距离),∴A错误;
根据椭圆的第二定义是平面内到定点距离与到定直线的距离之比为常数的点的集合(定点不在定直线上,该常数为小于1的正数),判断B、C错误;
判断D正确.
故选:D.
根据椭圆的第二定义是平面内到定点距离与到定直线的距离之比为常数的点的集合(定点不在定直线上,该常数为小于1的正数),判断B、C错误;
判断D正确.
故选:D.
点评:本题考查了椭圆的第一、第二定义的应用问题,解题时应理解这两个定义是等价的,属于基础题目.

练习册系列答案
相关题目
复数
(i是虚数单位)在复平面内对应的点位于( )
| 25 |
| 3-4i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
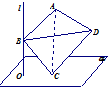 如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,
如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,