题目内容
14.如图,AB=AC=BD=1,AB?平面α,AC⊥平面α,BD⊥AB,BD与平面α成30°角,则C、D间的距离为$\sqrt{2}$
分析 由题意,作DD′⊥面α,垂足为D′,连接AD′,过D作DE⊥AC,垂足为E,求出DE、CE,即可求出C、D间的距离.
解答 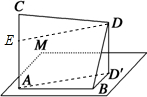 解:由题意,作DD′⊥面α,垂足为D′,连接AD′,则∠DBD′=30°,BD′⊥AB,
解:由题意,作DD′⊥面α,垂足为D′,连接AD′,则∠DBD′=30°,BD′⊥AB,
∵BD=1,∴DD′=$\frac{1}{2}$,BD′=$\frac{\sqrt{3}}{2}$,
∵AB=1,∴AD′=$\frac{\sqrt{7}}{2}$,
过D作DE⊥AC,垂足为E,则DE=AD′=$\frac{\sqrt{7}}{2}$,CE=$\frac{1}{2}$,
∴CD=$\sqrt{C{E}^{2}+C{D}^{2}}=\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查点、线、面间的距离计算,考查学生的计算能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
2.设是a,b两条不同的直线,α,β是两个不同的平面,且a?α,b?β,( )
| A. | 若α⊥β,则a⊥β | B. | 若α⊥β,则a⊥b | C. | 若α∥β,则a∥b | D. | 若α∥β,则a∥β |
9.已知点A(0,-1),抛物线C:y2=2px(p>0)的焦点为F,直线AF与抛物线C在第一象限交于M点,$\overrightarrow{AF}=\overrightarrow{FM}$,O为坐标原点,则△OAM的面积为( )
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
19.若函数f(x)=Asin($\frac{π}{2}$x+φ)(A>0)满足f(1)=0,则( )
| A. | f(x-2)一定是奇函数 | B. | f(x+1)一定是偶函数 | ||
| C. | f(x+3)一定是偶函数 | D. | f(x-3)一定是奇函数 |
6.直线y=x+b平分圆x2+y2-8x+2y-2=0的周长,则b=( )
| A. | 3 | B. | 5 | C. | -3 | D. | -5 |