题目内容
19．椭圆$\frac{x^2}{9}$+$\frac{y^2}{4}$=1上一点M到直线x+2y-10=0的距离的最小值为（ ）| A． | 2 | B． | $\sqrt{5}$ | C． | 2$\sqrt{5}$ | D． | 1 |
分析 设出与直线x+2y-10=0平行的直线方程为直线x+2y+m=0，联立直线方程与椭圆方程，由判别式等于0求得m值，再由两点间的距离公式得答案．
解答 解：设与直线x+2y-10=0平行的直线方程为直线x+2y+m=0，
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\\{x+2y+m=0}\end{array}\right.$，得25x2+18mx+9m2-144=0．
由（18m）2-100（9m2-144）=0，得576m2=14400，
解得m=±5．
当m=-5时，直线方程为x+2y-5=0，
此时两直线x+2y-10=0与直线x+2y-5=0的距离d=$\frac{|-10+5|}{\sqrt{5}}=\sqrt{5}$．
即椭圆$\frac{x^2}{9}$+$\frac{y^2}{4}$=1上一点M到直线x+2y-10=0的距离的最小值为$\sqrt{5}$．
故选：B．
点评 本题考查椭圆的简单性质，考查直线与椭圆位置关系的应用，体现了数学转化思想方法，是中档题．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
9．已知点A（0，-1），抛物线C：y2=2px（p＞0）的焦点为F，直线AF与抛物线C在第一象限交于M点，$\overrightarrow{AF}=\overrightarrow{FM}$，O为坐标原点，则△OAM的面积为（ ）
| A． | 1 | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{2}}}{4}$ |
8．
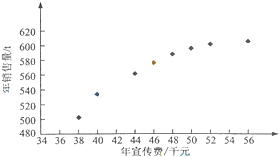某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到如图的散点图及一些统计量的值．
表中${w_i}=\sqrt{x_i}$，$\overrightarrow w$=$\frac{1}{8}$$\sum_{i=1}^8{w_i}$
（Ⅰ）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利率z与x、y的关系为z=0.2y-x．根据（Ⅱ）的结果回答下列问题：
（ⅰ）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ⅱ）年宣传费x为何值时，年利率的预报值最大？
附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：$\stackrel{∧}{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）}$，$\stackrel{∧}{α}$=$\overline{v}$-$\stackrel{∧}{β}$$\overline{u}$．
某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到如图的散点图及一些统计量的值．| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$（xi-$\overline{x}$）2 | $\sum_{i=1}^{8}$（wi-$\overline{w}$）2 | $\sum_{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$） | $\sum_{i=1}^{8}$（wi-$\overline{w}$）（yi-$\overline{y}$） |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
（Ⅰ）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利率z与x、y的关系为z=0.2y-x．根据（Ⅱ）的结果回答下列问题：
（ⅰ）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ⅱ）年宣传费x为何值时，年利率的预报值最大？
附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：$\stackrel{∧}{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{i}-\overline{u}）}$，$\stackrel{∧}{α}$=$\overline{v}$-$\stackrel{∧}{β}$$\overline{u}$．
9．若等差数列{an}中，a3=3，则{an}的前5项和S5等于（ ）
| A． | 10 | B． | 15 | C． | 20 | D． | 30 |