Question

平面内边长为

2

的等边△PAC与等腰Rt△ABC的公共边为AC，∠B=90°，沿AC所在直线把△ABC折起，使PB=

3

，若三棱锥P-ABC的四个顶点都在球O的表面上，则球O的表面积为

 

．

Answer 1

考点：二面角的平面角及求法,球的体积和表面积,球内接多面体

专题：球

分析：由题意画出图形，确定球O与平面ABC以及平面ACP的关系，通过余弦定理以及勾股定理，求出球的半径即可求出球的表面积．

解答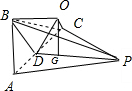： 解：由题意可知AP=PC=AP=

2

，∠ABC=90°，PB=

3

，
三棱锥P-ABC的四个顶点都在球O的表面上，
△APC的中心为：G，OG⊥平面APC，△ABC的外心是斜边AC的中点D，连结BD，
∴BD=

2

2

，
连结OB，PD，OD，DP=

6

2

，DG=

6

6

，则OD⊥平面ABC，
由余弦定理可知：BP²=BD²+DP²-2DB•DPcos∠BDP，cos∠BDP=

( 6 2 )2+( 2 2 )2-( 3 )2

2× 2 2 × 6 2

=-

3

3

，
∴sin∠ODG=-cos∠BDP=

3

3

，
OD=

DG

cos∠ODG

=

2 2

1-( 3 3 )2

=

3

2

，
设外接球的半径为R，则R=OB，
∴OB²=BD²+OD²，
∴R²=(

2

2

)2+(

3

2

)2=

7

4

，
∴R=

7

2

．
∴球O的表面积为：4πR²=7π．
故答案为：7π．

点评：本题考查几何体的外接球的表面积的求法，余弦定理以及勾股定理的应用，考查空间想象能力以及计算能力．