题目内容
不等式log2（-x2+2x+5）＞1的解集为A，不等式
＜1的解集为B．
（1）求A∩B；
（2）若不等式x2+ax+b＜0的解集为A∩B，求a和b的值．
| 2x+1 |
| x+3 |
（1）求A∩B；
（2）若不等式x2+ax+b＜0的解集为A∩B，求a和b的值．
考点：指、对数不等式的解法,一元二次不等式的解法
专题：不等式的解法及应用
分析：（1）由-x2+2x+5＞2求得x的范围，可得A=（-1，3）．由
＜1 得
＜0，解得x的范围可得B，从而求得A∩B．
（2）由不等式x2+ax+b＜0的解集为（-1，2），可得-1和2是x2+ax+b=0的实数根，再利用一元二次方程根与系数的关系，求出a、b的值．
| 2x+1 |
| x+3 |
| x-2 |
| x+3 |
（2）由不等式x2+ax+b＜0的解集为（-1，2），可得-1和2是x2+ax+b=0的实数根，再利用一元二次方程根与系数的关系，求出a、b的值．
解答：
解：（1）由-x2+2x+5＞2可得 x2-2x-3＜0，
求得-1＜x＜3，∴A=（-1，3）．
由
＜1 得：
＜0，解得-3＜x＜2，∴B=（-3，2），
∴A∩B=（-1，2）．
（2）由不等式x2+ax+b＜0的解集为（-1，2），可得-1和2是x2+ax+b=0的实数根，
所以
，解得
．
求得-1＜x＜3，∴A=（-1，3）．
由
| 2x+1 |
| x+3 |
| x-2 |
| x+3 |
∴A∩B=（-1，2）．
（2）由不等式x2+ax+b＜0的解集为（-1，2），可得-1和2是x2+ax+b=0的实数根，
所以
|
|
点评：本题主要考查对数不等式、分式不等式的解法，两个集合的交集的定义和求法，一元二次方程根与系数的关系，属于中档题．
练习册系列答案
相关题目
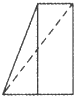
如图甲，将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD，得到几何体BCDEF，如图乙，则该几何体的正视图（或称主视图）是（ ）
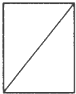
已知椭圆C1：