题目内容
已知(1-2x)7=a0+a1x+ax22+…+a7x7,
(1)求a0+a1+…+a7的值;
(2)求a0+a2+a4+a6及a1+a3+a5+a7的值;
(3)求各项二项式系数和;
(4)求二项式系数最大的项.
(1)求a0+a1+…+a7的值;
(2)求a0+a2+a4+a6及a1+a3+a5+a7的值;
(3)求各项二项式系数和;
(4)求二项式系数最大的项.
考点:二项式定理的应用
专题:二项式定理
分析:(1)在所给的等式中,令x=1,可得a0+a1+…+a7 的值;
(2)在所给的等式中,令x=-1,则a0-a1+a2-a3…-a7 的值,从而求得a0+a2+a4+a6和a1+a3+a5+a7 的值.
(3)各项二项式系数和为27,计算可得结果.
(4)由于n=7,故当r=3或4时,二项式系数最大,根据通项公式求得二项式系数最大的项.
(2)在所给的等式中,令x=-1,则a0-a1+a2-a3…-a7 的值,从而求得a0+a2+a4+a6和a1+a3+a5+a7 的值.
(3)各项二项式系数和为27,计算可得结果.
(4)由于n=7,故当r=3或4时,二项式系数最大,根据通项公式求得二项式系数最大的项.
解答:
解:(1)在(1-2x)7=a0+a1x+ax22+…+a7x7中,令x=1,可得a0+a1+…+a7 =-1 ①.
(2)令x=-1,则a0-a1+a2-a3…-a7 =2187 ②,
于是由①②求得a0+a2+a4+a6=1093,a1+a3+a5+a7的=-1094.
(3)各项二项式系数和为27=128,
(4)由于n=7,故当r=3或4时,二项式系数最大,故二项式系数最大的项为T4=-280x3 ;T5=560x4.
(2)令x=-1,则a0-a1+a2-a3…-a7 =2187 ②,
于是由①②求得a0+a2+a4+a6=1093,a1+a3+a5+a7的=-1094.
(3)各项二项式系数和为27=128,
(4)由于n=7,故当r=3或4时,二项式系数最大,故二项式系数最大的项为T4=-280x3 ;T5=560x4.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
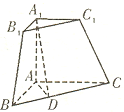 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,直线A1A⊥平面ABC,A1A=
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,直线A1A⊥平面ABC,A1A=