题目内容
在等比数列{an}中,公比q=2,且a2+a3=12.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前2015项和S2015.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前2015项和S2015.
考点:数列的求和,等比数列的前n项和
专题:等差数列与等比数列
分析:(I)利用等比数列的通项公式即可得出;
(II)利用等比数列的前n项和公式即可得出.
(II)利用等比数列的前n项和公式即可得出.
解答:
解:(Ⅰ)设等比数列{an}的公比q=2,且a2+a3=12,
∴2a1+4a1=12,
解得a1=2,
∴an=2n.
(Ⅱ)由(Ⅰ)知a1=2,q=2,
S2015=
=
=22016-2.
∴2a1+4a1=12,
解得a1=2,
∴an=2n.
(Ⅱ)由(Ⅰ)知a1=2,q=2,
S2015=
| a1(1-q2015) |
| 1-q |
| 2(1-22015) |
| 1-2 |
点评:本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
若数列{an}满足:a1=1,an+1=2an(n∈N*),则a5=( )
| A、8 | B、16 | C、32 | D、9 |
设方程ex=|ln(-x)|(其中e为自然对数的底数)的两个根分别为x1,x2,则( )
| A、x1x2<0 |
| B、x1x2=0 |
| C、x1x2>0 |
| D、0<x1x2<1 |
已知数列1
,3
,5
,7
,…则其前n项和Sn为( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
A、n2+1-
| ||
B、n2+2-
| ||
C、n2+1-
| ||
D、n2+2-
|
已知函数f(x)=-x2+2ex-x-
+m (x>0),若f(x)=0有两个相异实根,则实数m的取值范围是( )
| e2 |
| x |
| A、(-e2+2e,0) |
| B、(-e2+2e,+∞) |
| C、(0,e2-2e) |
| D、(-∞,-e2+2e) |
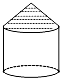 一粮仓如图所示,圆柱底面直径为12m,粮仓高4m,圆柱高与圆锥高相等,现拟建一个更大的粮仓,结构不变,现有两种方案:一是新建的仓库的底面直径比原来大2m(高不变);二是高度增加2m(底面直径不变).分别计算按这两种方案所建仓库的表面积(精确到0.01m2)
一粮仓如图所示,圆柱底面直径为12m,粮仓高4m,圆柱高与圆锥高相等,现拟建一个更大的粮仓,结构不变,现有两种方案:一是新建的仓库的底面直径比原来大2m(高不变);二是高度增加2m(底面直径不变).分别计算按这两种方案所建仓库的表面积(精确到0.01m2)