题目内容
已知首项为正数的等差数列{an}的前n项和为Sn,若a1006,a1007是方程x2-2012x-2011=0的两根,则使Sn>0成立的正整数n的最大值是( )
| A、1006 | B、1007 |
| C、2011 | D、2012 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:根据韦达定理判断出a1006+a1007=2012>0,a1006a1007=-2011<0,根据数列的首项为正判断出a1006>0,a1007<0,进而利用等差数列求和公式分别判断出S2012>0,S2013<0,进而可判断出使Sn>0成立的正整数n的最大值.
解答:
解:依题意知a1006+a1007=2012>0,a1006a1007=-2011<0,
∵数列的首项为正数,
∴a1006>0,a1007<0,
∴S2012=
=
>0,
S2013=
=a1007×2013<0,
∴使Sn>0成立的正整数n的最大值是2012,
故选:D.
∵数列的首项为正数,
∴a1006>0,a1007<0,
∴S2012=
| (a1+a2012)×2012 |
| 2 |
| (a1006+a1007)×2012 |
| 2 |
S2013=
| (a1+a2013)×2013 |
| 2 |
∴使Sn>0成立的正整数n的最大值是2012,
故选:D.
点评:本题主要考查了等差数列的性质.解题的关键的判断出Sn>0,Sn+1<0.

练习册系列答案
相关题目
“直线y=kx+b过点(1,1)”是“k=2且b=-1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f(x)=x2-tan(
-α)•x+1在[
,+∞)上单调递增,则α的取值范围是( )
| π |
| 6 |
| ||
| 2 |
A、[kπ-
| ||||
B、(kπ-
| ||||
C、(-
| ||||
D、(-∞,kπ+
|
(
+
)50的二项展开式中,整数项的个数是( )
| 3 | 2 |
| 1 | ||
|
| A、3 | B、4 | C、5 | D、6 |
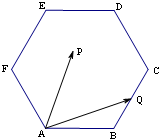 如图,在正六边形ABCDEF中,AB=2,点Q为BC边的中点,点P在正六边形ABCDEF内(含边界),则
如图,在正六边形ABCDEF中,AB=2,点Q为BC边的中点,点P在正六边形ABCDEF内(含边界),则