题目内容

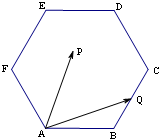如图，在正六边形ABCDEF中，AB=2，点Q为BC边的中点，点P在正六边形ABCDEF内（含边界），则
AP
•
AQ
的最大值为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积定义和投影的定义即可得出．
解答： 解：建立如图所示的直角坐标系，可得A（0，0）B（2，0），C（3，
3
），Q（
5
2
，
3
2
）.
AQ
=(
5
2
，
3
2
)
AP
•
AQ
的几何意义是
AP
在
AQ
方向上的投影与|
AQ
|的乘积，由图形可知，P与C重合时
AP
•
AQ
最大．
AP
=
AC
=(3，
3
)，
∴
AP
•
AQ
的最大值为：(
5
2
，
3
2
)•(3，
3
)=9．
故答案为：9．
点评：本题考查了数量积定义和投影的定义，属于中档题．
练习册系列答案
相关题目
把下列参数方程化为普通方程，并说明它们各表示什么曲线：
（1）
x=4cosφ
y=-5sinφ
（φ为参数）；       
（2）
x=1-4t
y=2t
（t为参数）
某中学有4位学生申请A，B，C三所大学的自主招生．若每位学生只能申请其中一所大学，且申请其中任何一所大学是等可能的．则被申请大学的个数X的数学期望E（X）=
 
．
已知向量
a
=（3，4）与
b
=（x，-8）共线．则|
b
|=
 
．
已知
2
5
=
1
3
+
1
15
，
2
7
=
1
4
+
1
28
，
2
9
=
1
5
+
1
45
，…观察以上各等式有：
（1）
2
11
=
 
；
（2）n≥3，且n∈N*时，
2
2n-1
=
 
．
一个扇形的弧长和面积均为5，则这个扇形圆心角的弧度数是
 
．
已知首项为正数的等差数列{an}的前n项和为Sn，若a1006，a1007是方程x2-2012x-2011=0的两根，则使Sn＞0成立的正整数n的最大值是（　　）
A、1006B、1007
C、2011D、2012
在△ABC中，BC=2，B=
π
3
，当△ABC的面积等于
3
2
时，AB=（　　）
A、
3
2
B、
1
2
C、1
D、
3
设函数f（x）=sin（ωx+
π
4
）（ω＞0）与函数g（x）=cos（2x+φ）（|φ|≤
π
2
）的对称轴完全相同，则φ的值为（　　）
A、
π
4
B、-
π
4
C、
π
2
D、-
π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网