题目内容
点E,F是正△ABC的边BC上的点,且BE=EF=FC,则tan∠EAF= .
考点:两角和与差的正切函数
专题:解三角形
分析:设出BE,则AB可表示,进而利用余弦定理求得AE,AF,进而根据余弦定理求得cos∠EAF,利用同角三角函数基本关系求得sin∠EAF和tan∠EAF.
解答:
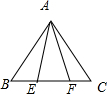 解:设BE=t,则AB=3t,
解:设BE=t,则AB=3t,
∴由余弦定理知AE=AF=
=
t,
∴cos∠EAF=
=
=
,
∵∠EAF<
,
∴sin∠EAF=
=
,
∴tan∠EAF=
=
.
故答案为:
.
 解:设BE=t,则AB=3t,
解:设BE=t,则AB=3t,∴由余弦定理知AE=AF=
9t2+t2-2×3t×t×
|
| 7 |
∴cos∠EAF=
| AE2+AF2-EF2 |
| 2•AE•AF |
| 7t2+7t2-t2 |
| 2•7t2 |
| 13 |
| 14 |
∵∠EAF<
| π |
| 2 |
∴sin∠EAF=
| 1-cos2∠EAF |
3
| ||
| 14 |
∴tan∠EAF=
| sin∠EAF |
| cos∠EAF |
3
| ||
| 13 |
故答案为:
3
| ||
| 13 |
点评:本题主要考查了余弦定理的应用.已知三边求角,一般采用余弦定理.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知首项为正数的等差数列{an}的前n项和为Sn,若a1006,a1007是方程x2-2012x-2011=0的两根,则使Sn>0成立的正整数n的最大值是( )
| A、1006 | B、1007 |
| C、2011 | D、2012 |
如图在△ABC中,MN∥BC,MC,NB交于点O,则图中相似三角形的对数为( )


| A、1 | B、2 | C、3 | D、4 |
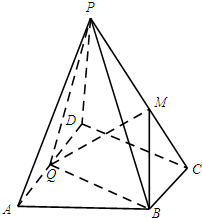 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,BC= 如图,圆O上一点C在直径AB上的射影为D.AD=2,AC=2
如图,圆O上一点C在直径AB上的射影为D.AD=2,AC=2