题目内容
在△ABC中，三个内角A，B，C的对边分别为a，b，c，且bsinA=
acosB．
（1）求角B；
（2）若a=1，SABC=
，求b．
| 3 |
（1）求角B；
（2）若a=1，SABC=
| 3 |
考点：余弦定理,正弦定理
专题：计算题,三角函数的求值,解三角形
分析：（1）运用正弦定理，结合同角的正切公式，即可得到B；
（2）运用三角形的面积公式和余弦定理，即可得到b的值．
（2）运用三角形的面积公式和余弦定理，即可得到b的值．
解答：
解：（1）由bsinA=
acosB，
即由正弦定理得，sinBsinA=
sinAcosB，
则tanB=
=
，
由B∈（0，π），即有B=
；
（2）由于a=1，S△ABC=
，B=
，
则S△ABC=
acsinB=
×
c=
，
则c=4，
即有b2=a2+c2-2accosB
=1+16-2×1×4×
=13，
故b=
．
| 3 |
即由正弦定理得，sinBsinA=
| 3 |
则tanB=
| sinB |
| cosB |
| 3 |
由B∈（0，π），即有B=
| π |
| 3 |
（2）由于a=1，S△ABC=
| 3 |
| π |
| 3 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则c=4，
即有b2=a2+c2-2accosB
=1+16-2×1×4×
| 1 |
| 2 |
故b=
| 13 |
点评：本题考查正弦定理和余弦定理的运用，考查三角形的面积公式及应用，以及同角公式的运用，考查运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
两个非零向量
，
垂直的充要条件是（ ）
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、（
|
已知命题p：实数x满足logax＞loga（2-x），其中0＜a＜1，则使命题p成立的必要不充分条件是（ ）
| A、1＜x＜2 | ||
| B、0＜x＜1 | ||
| C、-1＜x＜1 | ||
D、
|
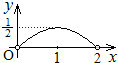
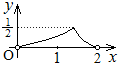
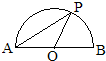如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=2，设弦AP的长为x，△APO的面积为y，则下列图象中，能表示y与x函数关系的图象大致是（ ）
