题目内容
已知函数f(x)=
,其导函数记为f′(x),则f(2014)+f′(2014)+f(-2014)-f′(-2014)= .
| (x+1)2+sinx |
| x2+1 |
考点:导数的运算
专题:导数的概念及应用
分析:先分离常数,令g(x)=
,得到g(x)为奇函数,在求f′(-x)=-f′(x),问题得以解决.
| 2x+sinx |
| x2+1 |
解答:
解:f(x)=
=
=1+
,
设g(x)=
,则g(-x)=-g(x),
∵f′(x)=g′(x)=
=
=
+
,
∴f′(-x)=-f′(x),
∴f(2014)+f′(2014)+f(-2014)-f′(-2014)=2.
故答案为:2
| (x+1)2+sinx |
| x2+1 |
| x2+2x+1+sinx |
| x2+1 |
| 2x+sinx |
| x2+1 |
设g(x)=
| 2x+sinx |
| x2+1 |
∵f′(x)=g′(x)=
| (2+cosx)-(2x+sinx)•(2x) |
| (x2+1)2 |
| 2(1+x2)+cosx-2xsinx |
| (x2+1)2 |
| 2 |
| x2+1 |
| cox-2xsinx |
| (x2+1)2 |
∴f′(-x)=-f′(x),
∴f(2014)+f′(2014)+f(-2014)-f′(-2014)=2.
故答案为:2
点评:本题主要考查了导数的运算法则和函数的奇偶性,属于中档题.

练习册系列答案
相关题目
下列函数中,与函数y=
有相同值域的是( )
| 5 |
| x |
| A、y=5x | ||
| B、y=5x+5 | ||
C、y=
| ||
| D、y=x2+5 |
复数
(i为虚数单位)的虚部是( )
| -i |
| 2i-1 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
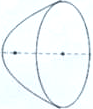 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线的焦点出,已知灯口直径是26厘米,灯深11厘米,那灯泡与反射镜的顶点距离为
汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线的焦点出,已知灯口直径是26厘米,灯深11厘米,那灯泡与反射镜的顶点距离为