题目内容
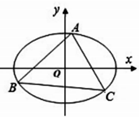 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)△ABC的三个顶点都在椭圆上,且△ABC的重心是原点O,证明:△ABC的面积是定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,由此能求出椭圆C的方程.
(2)设A(x1,y1),B(x2,y2),C(x3,y3),由△ABC重心是原点,得x3=-(x1+x2),y3=-(y1+y2),设直线AB的方程为y=kx+m,由
,得x2+4(kx+m)2=4,由此能求出△ABC的面积是定值
.
|
(2)设A(x1,y1),B(x2,y2),C(x3,y3),由△ABC重心是原点,得x3=-(x1+x2),y3=-(y1+y2),设直线AB的方程为y=kx+m,由
|
3
| ||
| 2 |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)经过点(1,
),
椭圆C的离心率e=
,
∴
,解得a2=4,b2=1,c2=3,
∴椭圆C的方程为
+y2=1.
(2)证明:设A(x1,y1),B(x2,y2),C(x3,y3),
∵△ABC重心是原点,∴
=0,
=0,
∴x3=-(x1+x2),y3=-(y1+y2),
当直线AB的斜率不存在时,A(-1,
),B(-1,-
),C(2,0),
或A(1,
),B(1,-
),C(-2,0),此时S△ABC=
.
当直线AB的斜率存在时,设直线AB的方程为y=kx+m,
由
,得x2+4(kx+m)2=4,
(1+4k2)x2+8kmx+4m2-4=0,
x1+x2=-
,x1x2=
,
y1+y2=k(x1+x2)+2m=-
+2m=
,
∴x3=
,y3=-
,
∵C(x3,y3)在椭圆上,∴(
)2+4(-
)2=4,
∴4m2=4k2+1,
∵|AB|=
=
=
,
点C(x3,y3)到直线AB的距离d=
=
,
∴S△ABC=
|AB|d=
•
•
=
=
=
.
综上所述,△ABC的面积是定值
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
椭圆C的离心率e=
| ||
| 2 |
∴
|
∴椭圆C的方程为
| x2 |
| 4 |
(2)证明:设A(x1,y1),B(x2,y2),C(x3,y3),
∵△ABC重心是原点,∴
| x1+y1+z1 |
| 3 |
| y1+y2+y3 |
| 3 |
∴x3=-(x1+x2),y3=-(y1+y2),
当直线AB的斜率不存在时,A(-1,
| ||
| 2 |
| ||
| 2 |
或A(1,
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
当直线AB的斜率存在时,设直线AB的方程为y=kx+m,
由
|
(1+4k2)x2+8kmx+4m2-4=0,
x1+x2=-
| 8km |
| 1+4k2 |
| 4m2-4 |
| 1+4k2 |
y1+y2=k(x1+x2)+2m=-
| 8k2m |
| 1+4k2 |
| 2m |
| 1+4k2 |
∴x3=
| 8km |
| 1+4k2 |
| 2m |
| 1+4k2 |
∵C(x3,y3)在椭圆上,∴(
| 8km |
| 1+4k2 |
| 2m |
| 1+4k2 |
∴4m2=4k2+1,
∵|AB|=
| 1+k2 |
| ||
| 1+4k2 |
=
| 1+k2 |
4
| ||
| 1+4k2 |
=
| 1+k2 |
4
| ||
| 1+4k2 |
点C(x3,y3)到直线AB的距离d=
|
| ||||
|
| |3m| | ||
|
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
4
| ||
| 1+4k2 |
| |3m| | ||
|
=
6
| ||
| 1+4k2 |
6
| ||
| 4m2 |
3
| ||
| 2 |
综上所述,△ABC的面积是定值
3
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查三角形面积是否为定值的判断与求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
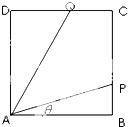 经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且∠PAQ=
经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且∠PAQ=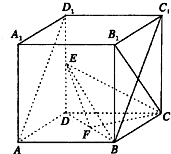 如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.
如图所示,在棱长为1的正方体AC1中,E,F分别为DD1,DB的中点.