题目内容
设a＞0，b＞0，a+4b+ab=3，则ab的最大值为 ．
考点：基本不等式
专题：不等式的解法及应用
分析：由基本不等式可得3=a+4b+ab≥2
+ab，整理可得
的一元二次不等式，解不等式可得
的取值范围，进而可得ab的取值范围，可得答案．
| a•4b |
| ab |
| ab |
解答：
解：∵a＞0，b＞0，a+4b+ab=3，
∴3=a+4b+ab≥2
+ab，
整理可得(
)2+4
-3≤0，
∵关于
的一元二次方程(
)2+4
-3=0的两根为-2±
，
∴不等式的解集为-2-
≤
≤-2+
，
∵a＞0，b＞0，∴0＜
≤-2+
，
∴0＜ab≤11-4
，
当且仅当a=4b时取等号，ab取最大值11-4
，
故答案为：11-4
∴3=a+4b+ab≥2
| a•4b |
整理可得(
| ab |
| ab |
∵关于
| ab |
| ab |
| ab |
| 7 |
∴不等式的解集为-2-
| 7 |
| ab |
| 7 |
∵a＞0，b＞0，∴0＜
| ab |
| 7 |
∴0＜ab≤11-4
| 7 |
当且仅当a=4b时取等号，ab取最大值11-4
| 7 |
故答案为：11-4
| 7 |
点评：本题考查基本不等式，涉及一元二次不等式的解集，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆C：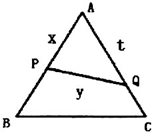
已知△ABC是边长为2的正三角形，P、Q依次是AB、AC边上的点，且线段PQ将△ABC分成面积相等的两部分．设AP=x，AQ=t，PQ=y，求：