题目内容
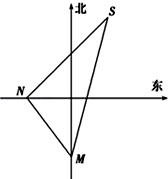 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为考点:解三角形的实际应用
专题:应用题,解三角形
分析:根据题意画出相应的图形,在三角形PMN中,根据sin∠MPN与sin∠PNM的值,以及PM的长,利用正弦定理求出MN的长,除以时间即可确定出速度.
解答:
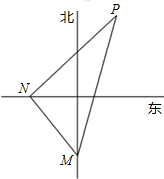 解:由题意知PM=20海里,∠NMP=45°,
解:由题意知PM=20海里,∠NMP=45°,
∴PM与正东方向的夹角为75°,MN与正东方向的夹角为60°,
∴∠PNM=105°,
∴∠MPN=30°,
∵sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
,
∴在△MNP中利用正弦定理可得,
=
解得:MN=10(
-
)海里,
∴货轮航行的速度v=
=20(
-
)海里/小时.
故答案为:20(
-
)
 解:由题意知PM=20海里,∠NMP=45°,
解:由题意知PM=20海里,∠NMP=45°,∴PM与正东方向的夹角为75°,MN与正东方向的夹角为60°,
∴∠PNM=105°,
∴∠MPN=30°,
∵sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
| ||||
| 4 |
∴在△MNP中利用正弦定理可得,
| MN |
| sin30° |
| 20 |
| sin105° |
解得:MN=10(
| 6 |
| 2 |
∴货轮航行的速度v=
10(
| ||||
|
| 6 |
| 2 |
故答案为:20(
| 6 |
| 2 |
点评:此题考查了正弦定理在解三角形中的应用,解决实际问题的关键是要把实际问题转化为数学问题,然后利用数学知识进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若直线ax+by+c=0(ab≠0)在两坐标轴上的截距相等,则a,b,c满足的条件是( )
| A、a=b |
| B、|a|=|b| |
| C、c=0或a=b |
| D、c=0或|a|=|b| |
已知数列{an}为等差数列,若
<-1,且它们的前n项和Sn有最大值,则使得Sn>0的n的最大值为( )
| a11 |
| a10 |
| A、21 | B、20 | C、19 | D、18 |
设a>0,b>0.若2a•2b=2,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、8 | ||
| B、4 | ||
| C、1 | ||
D、
|
在等比数列{an}中,首项a1<0,则{an}是递增数列的充要条件是公比( )
| A、q>1 | B、q<1 |
| C、0<q<1 | D、q<0 |