题目内容
8.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$2\sqrt{3}$,AB=2,AC=1,∠BAC=60°,则此球的表面积等于( )| A. | 5π | B. | 20π | C. | 8π | D. | 16π |
分析 画出球的内接直三棱ABC-A1B1C1,作出球的半径,然后可求球的表面积.
解答 解:设棱柱的高为h,则$\frac{1}{2}×2×1×\frac{\sqrt{3}}{2}×h=2\sqrt{3}$,∴h=4.
∵AB=2,AC=1,∠BAC=60°,
∴BC=$\sqrt{3}$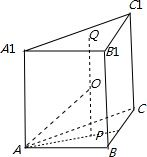
如图,连接上下底面外心,O为PQ的中点,OP⊥平面ABC,
则球的半径为OA,
由题意,AP=$\frac{1}{2}$•$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=1,OP=2,
∴OA=$\sqrt{4+1}$=$\sqrt{5}$,
所以球的表面积为:4πR2=20π.
故选:B.
点评 本题考查球的体积和表面积,球的内接体问题,考查学生空间想象能力理解失误能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.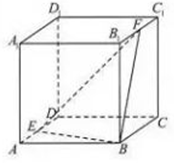 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )| A. | [0,1] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [1,2] | D. | [$\frac{3}{2}$,2] |
3.去A城市旅游有三条不同路线,甲、乙两位同学各自选择其中一条线路去A城市旅游,若每位同学选择每一条线路的可能性相同,则这两位同学选择同一条路线的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{9}$ |
20.已知数列{an}:a1=1,${a_{n+1}}=2{a_n}+3,({n∈{N^+}})$,则an=( )
| A. | 2n+1-3 | B. | 2n-1 | C. | 2n+1 | D. | 2n+2-7 |
17.已知b>0,log3b=a,log6b=c,3d=6,则下列等式成立的是( )
| A. | a=2c | B. | d=ac | C. | a=cd | D. | c=ad |
 已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.
已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.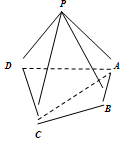 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△ADP是等腰直角三角形,∠APD是直角,AB⊥AD,AB=1,$AD=2,AC=CD=\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△ADP是等腰直角三角形,∠APD是直角,AB⊥AD,AB=1,$AD=2,AC=CD=\sqrt{5}$.