题目内容
7.已知F1、F2分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的左右两个焦点,过F1作倾斜角为$\frac{π}{4}$的弦AB,则△F2AB的面积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$-1 |
分析 求出直线AB的方程,代入椭圆方程,求得交点A,B的坐标,利用S=$\frac{1}{2}$•|F1F2|•|y1-y2|,即可得出S.
解答 解:椭圆$\frac{{x}^{2}}{2}$+y2=1的左右两个焦点(-1,0),过F1作倾斜角为$\frac{π}{4}$的弦AB,可得直线AB的方程为:y=x+1,
把 y=x+1 代入 x2+2y2=2 得3x2+4x=0,
解得x1=0 x2=-$\frac{4}{3}$,y1=1,y2=-$\frac{1}{3}$,
∴S=$\frac{1}{2}$•|F1F2|•|y1-y2|=$\frac{1}{2}×2×|1+\frac{1}{3}|$=$\frac{4}{3}$.
故选:B.
点评 本题考查了直线与椭圆相交问题、椭圆的标准方程及其性质、三角形的面积计算公式,考查了计算能力,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.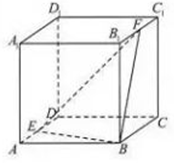 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )| A. | [0,1] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [1,2] | D. | [$\frac{3}{2}$,2] |
2.在等比数列{an}中,若a6=6,a9=9,则a3为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{16}{9}$ | D. | 4 |
17.已知b>0,log3b=a,log6b=c,3d=6,则下列等式成立的是( )
| A. | a=2c | B. | d=ac | C. | a=cd | D. | c=ad |