题目内容
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
=a,
=b,则
等于( )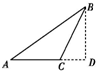
| AB |
| AC |
| BD |

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:向量在几何中的应用
专题:平面向量及应用
分析:直接利用三角形中的边角关系,利用向量表示即可.
解答:
解:如图所示,在直角三角形BCD中,∠BCD=60°,CD=
CB=
AC,
所以
=
=
b,
=
b,
所以
=
-
=
b-a.
故选:D.
| 1 |
| 2 |
| 1 |
| 2 |
所以
| CD |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AD |
| 3 |
| 2 |
所以
| BD |
| AD |
| AB |
| 3 |
| 2 |
故选:D.
点评:本题考查向量的几何中的应用,基本知识的考查.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知抛物线y2=2px(p>0)上一点P到焦点F的距离为p,到x轴的距离为1,过F作倾斜角为45°的直线l与抛物线的准线交于点A,则
•
等于( )
| OA |
| OF |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知F1,F2分别是双曲线
-
=1(a>0,b>0)的两个焦点,点P是双曲线上的一点,且满足∠F1PF2=90°.若△PF1F2的面积为4,且双曲线的离心率为
,则双曲线的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
sin
=( )
| 10π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|