Question

矩形ABCD中，AD=2，AB=3，E为AD的中点，P为边AB上一动点，则tan∠DPE的最大值为（　　）

• A、

  2

  2

• B、

  2

  3

• C、

  2

  4

• D、1

Answer 1

考点：正弦定理

专题：三角函数的求值,解三角形,不等式的解法及应用

分析：设AP=x，分别表示出tan∠DPA和tan∠EPA，通过两角和公式表示tan∠DPE，整理后利用基本不等式求得其最大值．

解答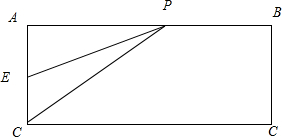： 解：设AP=x，x＞0，
则tan∠DPA=

2

x

，tan∠EPA=

1

x

，
∴tan∠DPE=tan（∠DPA-∠EPA）=

tan∠DPA-tan∠EPA

1+tan∠EPAtan•∠EPA

=

2 x - 1 x

1+ 2 x • 1 x

=

1

x+ 2 x

，
∵x+

2

x

≥2

2

，当且仅当x=

2

时，取等号，
0＜

1

x+ 2 x

≤

1

2 2

=

2

4

，即tan∠DPE≤

2

4

，
即tan∠DPE的最大值为

2

4

，
故选C．

点评：本题主要考查利用解三角形的问题．利用了设而不求的方式，借助三角函数恒等变换和基本不等式的性质解决问题．