题目内容
O为△ABC的外心,|
|=2,|
|=4,设
=x
+y
,若x+4y=2,则|
|的值为( )
| AB |
| AC |
| AO |
| AB |
| AC |
| AO |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、6 |
考点:向量加减混合运算及其几何意义
专题:平面向量及应用
分析:根据
=x
+y
,得|
|2=x
•
+y
•
,则,根据向量数量积的几何意义分别求出
•
,
•
后,得出关于x,y的代数式,利用x+4y=2整体求解.
| AO |
| AB |
| AC |
| AO |
| AB |
| AO |
| AC |
| AO |
| AB |
| AO |
| AC |
| AO |
解答:
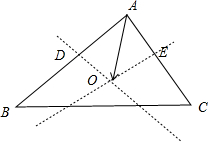
解:如图所示,∵
=x
+y
,
∴|
|2=x
•
+y
•
,
∵O为外心,D,E为中点,OD,OE分别为两中垂线,
∴
•
=|
|•|
|cos<
,
>=
|×
|=2×
×2=2,
同理求得
•
=8,
∴|
|2=2x+8y=2(x+4y)=2×2=4,
∴|
|=2.
故选A.
| AO |
| AB |
| AC |
∴|
| AO |
| AB |
| AO |
| AC |
| AO |
∵O为外心,D,E为中点,OD,OE分别为两中垂线,
∴
| AB |
| AO |
| AB |
| AO |
| AB |
| AO |
| |AB |
| |AD |
| 1 |
| 2 |
同理求得
| AC |
| AO |
∴|
| AO |
∴|
| AO |

故选A.
点评:本题考查了三角形外心的性质,向量数量积的运算、向量模的求解.本题中进行了合理的转化,并根据外心的性质化简求解.

练习册系列答案
相关题目
曲线f(x)=x3+x-2在M处的切线垂直于直线y=-
x-1,则M点的坐标为( )
| 1 |
| 4 |
| A、(1,0) |
| B、(2,8) |
| C、(1,0)和(-1,-4) |
| D、(2,8)和(-1,-4) |
矩形ABCD中,AD=2,AB=3,E为AD的中点,P为边AB上一动点,则tan∠DPE的最大值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
若集合M={-1,0,1},P={y|y=x2,x∈M},则集合M与P的关系是( )
| A、P?M | B、M?P |
| C、M=P | D、M∈P |
在锐角△ABC中,∠A=2∠B,∠A、∠B的对边长分别是a、b,则
的取值范围是( )
| b |
| b+a |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
某学生在高三学年最近九次考试中的数学成绩加下表:
设回归直线方程y=bx+a,则点(a,b)在直线x+5y-10=0的( )
| 第x考试 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 数学成绩y(分) | 121 | 119 | 130 | 106 | 131 | 123 | 110 | 124 | 116 |
| A、左上方 | B、左下方 |
| C、右上方 | D、右下方 |
下列函数f(x)中,满足“对任意的x1,x2∈(0,+∞)时,均有(x1-x2)[f(x1)-f(x2)]>0”的是( )
A、f(x)=
| ||
| B、f(x)=x2-4x+4 | ||
| C、f(x)=2x | ||
D、f(x)=log
|