题目内容
已知函数f（x）=
，满足?x1≠x2，都有
＜0成立，则a的取值范围是（ ）
|
| f(x1)-f(x2) |
| x1-x2 |
| A、（0，1） | ||
| B、（1，+∞） | ||
C、（0，
| ||
D、（0，
|
考点：函数单调性的性质
专题：计算题,函数的性质及应用
分析：先确定函数f（x）是R上的减函数，可得
，即可确定a的取值范围．
|
解答：
解：∵?x1≠x2，都有
＜0成立，
∴函数f（x）是R上的减函数，
∵函数f（x）=
，
∴
，
∴0＜a≤
，
故选：D．
| f(x1)-f(x2) |
| x1-x2 |
∴函数f（x）是R上的减函数，
∵函数f（x）=
|
∴
|
∴0＜a≤
| 1 |
| 4 |
故选：D．
点评：本题主要考查函数的单调性，确定函数f（x）是R上的减函数，得出
是关键．
|
练习册系列答案
相关题目
函数y=-|x|（x∈[-2，2]）的图象是（ ）
A、 |
B、 |
C、 |
D、 |
复数
等于（ ）
| 2+3i |
| 3-2i |
| A、-i | B、i |
| C、12-13i | D、12+13i |
已知函数f（x）=x（x-a）（x-b）的导函数为f′（x），且f′（0）=4，则a2+2b2的最小值为（ ）
| A、1 | ||
| B、4 | ||
C、2
| ||
D、8
|
已知x=
与x=
为函数f（x）=3sin（ωx+
）的两条相邻对称轴，则ω=（ ）
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |
若点P在曲线y=x3-x上移动，则过P点的切线的倾斜角的取值范围是（ ）
| A、[0，π） | ||||||
B、（0，
| ||||||
C、[0，
| ||||||
D、[0，
|
下列命题中，假命题的是（ ）
A、?x0∈R，sinx0+
| ||
| B、?x∈[0，+∞），ex-x＞0 | ||
| C、?x0∈（0，+∞），lgx0=-1 | ||
| D、?x∈（-∞，0]，2x2-3x-2＞0 |
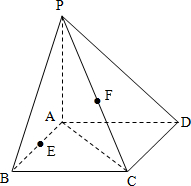已知PA⊥平面ABCD，四边形ABCD为正方形，PA=AB=4，E、F分别为AB、PC的中点．