题目内容
| ∫ | 1 0 |
| 1-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
考点:定积分
专题:导数的概念及应用
分析:先根据定积分的几何意义求出
(
dx,再根据定积分计算求出
xdx,问题得以解决.
| ∫ | 1 0 |
| 1-(x-1)2 |
| ∫ | 1 0 |
解答:
解:因为
(
dx表示以(1,0)为圆心,以1半径的圆的面积的四分之一,
故
(
dx=
π
∴
(
-x)dx=
(
dx-
xdx=
-
x2
=
-
故选:B.
| ∫ | 1 0 |
| 1-(x-1)2 |
故
| ∫ | 1 0 |
| 1-(x-1)2 |
| 1 |
| 4 |
∴
| ∫ | 1 0 |
| 1-(x-1)2 |
| ∫ | 1 0 |
| 1-(x-1)2 |
| ∫ | 1 0 |
| π |
| 4 |
| 1 |
| 2 |
| | | 1 0 |
| π |
| 4 |
| 1 |
| 2 |
故选:B.
点评:本题主要考查了定积分的几何意义和微积分基本定理,属于基础题.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、空间中的任意三点确定一个平面 |
| B、空间中两两相交的三条直线确定一个平面 |
| C、有且只有一组对边平行的四边形是平面图形 |
| D、两组对边分别相等的四边形一定是平面图形 |
化简
+
+
-
=( )
| AB |
| BD |
| CA |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x=
与x=
为函数f(x)=3sin(ωx+
)的两条相邻对称轴,则ω=( )
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |
已知锐角三角形的边长分别是3,5,x,则x的取值范围是( )
A、1<x<
| ||
B、4<x<
| ||
| C、1<x<4 | ||
D、4<x<
|
若点P在曲线y=x3-x上移动,则过P点的切线的倾斜角的取值范围是( )
| A、[0,π) | ||||||
B、(0,
| ||||||
C、[0,
| ||||||
D、[0,
|
以下棱柱中,最多只有一对面互相平行的是( )
| A、三棱柱 | B、四棱柱 |
| C、八棱柱 | D、六棱柱 |
不等式|2x-1|≤3的解集为( )
| A、{x|-1≤x≤2} |
| B、{x|x≥2或x≤-1} |
| C、{x|-2≤x≤1} |
| D、{x|x≥1或x≤-2} |
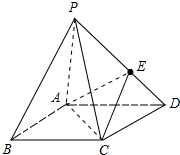 如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.