题目内容
请用分析法证明:已知0<a<1,则
+
≥9.
| 1 |
| a |
| 4 |
| 1-a |
考点:综合法与分析法(选修)
专题:证明题,分析法
分析:分析法是从结论出发找出要证结论的充分条件,即可得出结论.
解答:
证明:∵0<a<1,
∴1-a>0,
要证明
+
≥9,
即证明1-a+4a≥9a(1-a),
必须证(3a-1)2≥0
显然成立,故原不等式成立.
∴1-a>0,
要证明
| 1 |
| a |
| 4 |
| 1-a |
即证明1-a+4a≥9a(1-a),
必须证(3a-1)2≥0
显然成立,故原不等式成立.
点评:本题考查分析法,掌握分析法的证明步骤是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=x2+2ax+b2,若a∈[0,2],b∈[0,3],则函数f(x)有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线ax+(1-a)y=3与(a-1)x+(2a+3)y=2互相垂直,则a等于( )
| A、3 | ||
| B、1 | ||
C、0或-
| ||
| D、1或-3 |
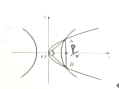 如图,双曲线
如图,双曲线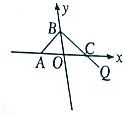 如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足
如图,已知A(-3p,0)(p>0),B,C两点分别在y轴和x轴上运动,并且满足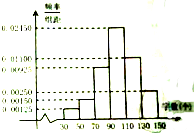 重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.
重庆Z中学为筹备参加“汉字听写比赛”,对初二年级的400名同学进行了一次摸底听写比赛,每位同学听写150个字,听写正确130个字以上(含130个)的同学才可以参加市级决赛.