题目内容

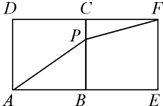
一个几何体的三视图如图所示，则它的体积为
 
．
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是四棱锥，根据三视图判断相关几何量的数据，把数据代入棱锥的体积公式计算．
解答： 解：由三视图知：几何体是四棱锥，如图：
其中SA⊥平面ABCD，SA=4，四边形ABCD为直角梯形，AD∥BC，AB=AD=4，BC=1．
∴几何体的体积V=
1
3
×
1+4
2
×4×4=
40
3
．
故答案为：
40
3
．
点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．
练习册系列答案
相关题目
某同学为了研究函数f（x）=
1+x2
+
1+(1-x)2
（0≤x≤1）的性质，构造了如图所示的两个边长为1的正方形ABCD和BEFC，点P是边BC上的一个动点，设CP=x，则f（x）=AP+PF．
（1）fmin（x）=
 
；
（2）函数f（x）=
22
2
的零点个数是
 
．
下表是关于新生婴儿的性别与出生时间段调查的列联表，那么，A=
 
，B=
 
，C=
 
，D=
 
．
晚上 白天 总计
男 45 A 92
女 B 35 C
总计 98 D 180
已知一个三角形的三边长分别是5，5，6，在三角形内任投一点，则该点距离三角形的三个顶点的距离均超过
1
π
的概率为
 
．
平面内有两定点A、B及动点P，设命题甲是：“|PA|+|PB|是定值”，命题乙是：“点P的轨迹是以A、B为焦点的椭圆”，那么甲是乙的
 
．
抛物线C：y2=4x上一点P（2，t）到焦点F的距离是
 
．
已知F1、F2为双曲线C：
x2
4
-y2=1的左、右焦点，点P在C上，∠F1PF2=60°，则P到x轴的距离为
 
．
假设关于某种设备的使用年限x和支出的维修费用y（万元），有以下的统计资料：
使用年限x 2 3 4 5 6
维修费用y 2.2 3.8 5.5 6.5 7.0
若维修费用y（万元）与使用年限x的线性回归方程是：
y
=1.23x+a，则a=
 
．
三角形ABC中，∠C=90°，AB=2，AC=1，若
AD
=
3
2
AB
，则
CD
•
CB
=（　　）
A、
3
2
B、
6
2
C、
3
2
D、
9
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网