题目内容
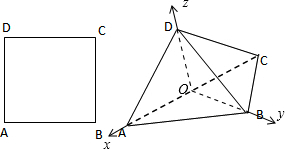
 如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:①△DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是
| ||
| 6 |
④AB与CD所成的角是60°.
其中正确命题的序号是
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:过D作DO⊥AC于O,连接BO,利用勾股定理求得BD长,可得①正确;
通过证明AC⊥平面BOD,证明AC⊥BD,可得②正确;
利用棱锥的体积公式计算三棱锥的体积,可得③错误;
建立空间直角坐标系,利用向量坐标运算求异面直线AB与CD所成的角,可得④正确.
通过证明AC⊥平面BOD,证明AC⊥BD,可得②正确;
利用棱锥的体积公式计算三棱锥的体积,可得③错误;
建立空间直角坐标系,利用向量坐标运算求异面直线AB与CD所成的角,可得④正确.
解答:
解:过D作DO⊥AC于O,连接BO,由题意知:DO=BO=
,
∵平面ADC⊥平面ABC,∴DO⊥平面ABC,∴DO⊥BO,∴BD=1,即△BCD为等边三角形,①正确;
∵O为AC的中点,AB=BC,∴BO⊥AC,∴AC⊥平面BOD,BD?平面BOD,∴AC⊥BD,②正确;
∵VD-ABC=
×
×1×1×
=
,∴③错误;
建立空间直角坐标系如图:
则
=(-
,
,0),
=(
,0,
),
∴cos<
,
>=-
,∴异面直线AB与CD所成的角是60°,∴④正确.
故答案为:①②④.
| ||
| 2 |
∵平面ADC⊥平面ABC,∴DO⊥平面ABC,∴DO⊥BO,∴BD=1,即△BCD为等边三角形,①正确;
∵O为AC的中点,AB=BC,∴BO⊥AC,∴AC⊥平面BOD,BD?平面BOD,∴AC⊥BD,②正确;
∵VD-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
建立空间直角坐标系如图:
则
| AB |
| ||
| 2 |
| ||
| 2 |
| CD |
| ||
| 2 |
| ||
| 2 |
∴cos<
| AB |
| CD |
| 1 |
| 2 |
故答案为:①②④.

点评:本题考查了面面垂直的性质及异面直线所成角的求法,考查了学生的空间想象能力与计算能力,要熟练掌握利用向量坐标运算求异面直线所成的角的方法.

练习册系列答案
相关题目
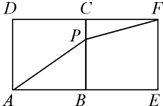 某同学为了研究函数f(x)=
某同学为了研究函数f(x)=