题目内容
若线段x+y=1(-1≤x≤1)与椭圆
+
=k(k>0)没有交点,则实数k的取值范围是 .
| x2 |
| 3 |
| y2 |
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:线段x+y=1(-1≤x≤1)与椭圆
+
=k(k>0)没有交点,则线段x+y=1(-1≤x≤1)在椭圆的内部或外部,分类讨论,可得结论.
| x2 |
| 3 |
| y2 |
| 2 |
解答:
解:∵线段x+y=1(-1≤x≤1)与椭圆
+
=k(k>0)没有交点,
∴线段x+y=1(-1≤x≤1)在椭圆的内部或外部,
线段x+y=1(-1≤x≤1)在椭圆的内部时,
,∴k>
;
线段x+y=1(-1≤x≤1)在椭圆的外部时,y=1-x代入
+
=k可得5x2-6x-6k+3=0,
∴△=36-20(-6k+3)<0,∵k>0,∴0<k<
.
综上所述,0<k<
或k>
.
故答案为:0<k<
或k>
.
| x2 |
| 3 |
| y2 |
| 2 |
∴线段x+y=1(-1≤x≤1)在椭圆的内部或外部,
线段x+y=1(-1≤x≤1)在椭圆的内部时,
|
| 7 |
| 3 |
线段x+y=1(-1≤x≤1)在椭圆的外部时,y=1-x代入
| x2 |
| 3 |
| y2 |
| 2 |
∴△=36-20(-6k+3)<0,∵k>0,∴0<k<
| 1 |
| 5 |
综上所述,0<k<
| 1 |
| 5 |
| 7 |
| 3 |
故答案为:0<k<
| 1 |
| 5 |
| 7 |
| 3 |
点评:本题考查线段与椭圆的位置关系,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
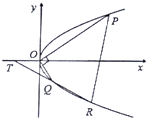 如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q
如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q
 某同学为了研究函数f(x)=
某同学为了研究函数f(x)=