题目内容
17．已知x，y满足满足约束条件$\left\{\begin{array}{l}x+y≤10\;\\ x-y≤2\;\\ x≥3\end{array}\right.$，那么z=x2+y2的最大值为58．分析 由约束条件作出可行域，由z=x2+y2的几何意义，即可行域内的动点与坐标原点距离的平方得答案．
解答 解：由约束条件$\left\{\begin{array}{l}x+y≤10\;\\ x-y≤2\;\\ x≥3\end{array}\right.$作出可行域如图，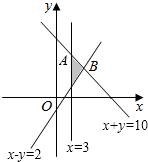
联立方程组$\left\{\begin{array}{l}{x=3}\\{x+y=10}\end{array}\right.$，解得：A（3，7）；
联立方程组$\left\{\begin{array}{l}{x+y=10}\\{x-y=2}\end{array}\right.$，解得：B（6，4）．
|OA|=$\sqrt{58}$，|OB|=$\sqrt{52}$．
坐标原点O到直线x+y=10的距离d=$\frac{|10|}{\sqrt{2}}=5\sqrt{2}$．
∴z=x2+y2的最大值为58．
故答案为：58．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
如图，设正三棱锥P-ABC的侧棱长为l，∠APB=30°，E，F分别是BP，CP上的点，则△AEF周长的最小值为$\sqrt{2}l$．
5．“a=1”是“函数f（x）=a|x|+b，b∈R在区间[0，+∞）上为增函数”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
9．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜2π）在一个周期内的部分对应值如下表：
（Ⅰ）求f（x）的解析式；
（Ⅱ）求函数g（x）=f（x）+2sinx的最大值和最小值．
| x | $-\frac{π}{2}$ | 0 | $\frac{π}{6}$ | $\frac{π}{2}$ |
| f（x） | -1 | 1 | $\frac{1}{2}$ | -1 |
（Ⅱ）求函数g（x）=f（x）+2sinx的最大值和最小值．