题目内容
点P为椭圆
+
=1与双曲线
-
=1的一个公共点,点F1,F2的坐标分别为(-3,0)和(3,0),求PF1、PF2.
| x2 |
| 36 |
| y2 |
| 27 |
| x2 |
| 4 |
| y2 |
| 5 |
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由于椭圆
+
=1与双曲线
-
=1有相同的焦点,且焦点F1,F2的坐标分别为(-3,0)和(3,0),则有PF1+PF2=12,且PF1-PF2=±4,解方程即可得到.
| x2 |
| 36 |
| y2 |
| 27 |
| x2 |
| 4 |
| y2 |
| 5 |
解答:
解:椭圆
+
=1与双曲线
-
=1有相同的焦点,
且焦点F1,F2的坐标分别为(-3,0)和(3,0),
由椭圆、双曲线的定义,可得,
PF1+PF2=2×6=12,且PF1-PF2=±4,
解得PF1=8,PF2=4或PF1=4,PF2=8.
| x2 |
| 36 |
| y2 |
| 27 |
| x2 |
| 4 |
| y2 |
| 5 |
且焦点F1,F2的坐标分别为(-3,0)和(3,0),
由椭圆、双曲线的定义,可得,
PF1+PF2=2×6=12,且PF1-PF2=±4,
解得PF1=8,PF2=4或PF1=4,PF2=8.
点评:本题考查椭圆和双曲线的方程、定义和性质,考查运算能力,属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
已知函数f(x)=
,若a>0,b>0,c>0,a+b>c,则( )
| x |
| x+1 |
| A、f(a)+f(b)>f(c) |
| B、f(a)+f(b)=f(c) |
| C、f(a)+f(b)<f(c) |
| D、以上结论都不对 |
已知x>0时,(x-1)f′(x)<0,若△ABC是锐角三角形,则一定成立的是( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)>f(cosB) |
 (理科)如图,边长为2的正方形ABCD和正方形ABEF所在的面所成角为60°,M和N分别是AC和BF上的点,且AM=FN,求线段MN长的取值范围( )
(理科)如图,边长为2的正方形ABCD和正方形ABEF所在的面所成角为60°,M和N分别是AC和BF上的点,且AM=FN,求线段MN长的取值范围( )| A、[0.5,2] | ||
| B、[1.5,2] | ||
C、[
| ||
| D、[1,2] |
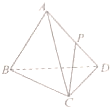 如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.
如图,正四面体ABCD(四个面是全等的等边三角形的四面体)中,P是AD的中点,求CP与平面DBC所成角的正弦值.