题目内容
 (理科)如图,边长为2的正方形ABCD和正方形ABEF所在的面所成角为60°,M和N分别是AC和BF上的点,且AM=FN,求线段MN长的取值范围( )
(理科)如图,边长为2的正方形ABCD和正方形ABEF所在的面所成角为60°,M和N分别是AC和BF上的点,且AM=FN,求线段MN长的取值范围( )| A、[0.5,2] | ||
| B、[1.5,2] | ||
C、[
| ||
| D、[1,2] |
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:设AM=FN=a(0≤a≤2
),则MP=
a,PN=2-
a,由余弦定理,表示出MN,即可得出结论.
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
 解:过M作MP⊥AB,垂足为P,连接PN,则∠MPN=60°
解:过M作MP⊥AB,垂足为P,连接PN,则∠MPN=60°
设AM=FN=a(0≤a≤2
),则MP=
a,PN=2-
a.
由余弦定理知:MN2=(
a)2+(2-
a)2-2×
a×(2-
a)×
=
(a-
)2+1
∵0≤a≤2
,∴1≤MN≤2.
故选:D.
 解:过M作MP⊥AB,垂足为P,连接PN,则∠MPN=60°
解:过M作MP⊥AB,垂足为P,连接PN,则∠MPN=60°设AM=FN=a(0≤a≤2
| 2 |
| ||
| 2 |
| ||
| 2 |
由余弦定理知:MN2=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| 2 |
∵0≤a≤2
| 2 |
故选:D.
点评:关键是将空间两点间的距离表示成a的函数,进而转化成求函数最值的问题.

练习册系列答案
相关题目
根据如下样本数据:
得到的线性回归方程为
=bx+a,则( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -1 | -1 | -2 |
| ? |
| y |
| A、a>0,b>0 |
| B、a>0,b<0 |
| C、a<0,b>0 |
| D、a<0,b<0 |
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=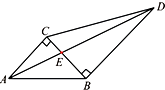 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.若记