Question

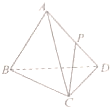如图，正四面体ABCD（四个面是全等的等边三角形的四面体）中，P是AD的中点，求CP与平面DBC所成角的正弦值．

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：作DE⊥BC，交BC于E，作AO⊥平在BDC，交DE于O，作PQ⊥平面BDC，交DE于Q，连结PC，CQ，则∠PCQ是CP与平面DBC所成角，由此能求出CP与平面DBC所成角的正弦值．

解答： 解：作DE⊥BC，交BC于E，作AO⊥平在BDC，交DE于O，
作PQ⊥平面BDC，交DE于Q，连结PC，CQ，
则∠PCQ是CP与平面DBC所成角，
设正四面体ABCD的棱长为2，
则DE=PC=DE=

22-12

=

3

，
DO=

2

3

DE=

2 3

3

，DQ=

3

3

，
AO=

4- 4 3

=

2 6

3

，PQ=

1

2

AO=

6

3

，
∴sin∠PCQ=

PQ

PC

=

6 3

3

=

2

3

．
∴CP与平面DBC所成角的正弦值为

2

3

．

点评：本题考查直线与平面所成角的正弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．