题目内容
17.若x≥0,y≥0,2x+3y≤10,2x+y≤6,则z=3x+2y的最大值是10.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答 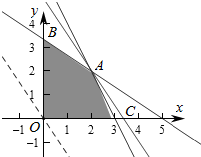 解:由z=3x+2y得$y=-\frac{3}{2}x+\frac{z}{2}$,
解:由z=3x+2y得$y=-\frac{3}{2}x+\frac{z}{2}$,
作出不等式组对应的平面区域如图(阴影部分):
平移直线$y=-\frac{3}{2}x+\frac{z}{2}$由图象可知当直线$y=-\frac{3}{2}x+\frac{z}{2}$经过点A时,直线$y=-\frac{3}{2}x+\frac{z}{2}$的截距最大,
此时z也最大,
由$\left\{\begin{array}{l}{2x+3y=10}\\{2x+y=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即A(2,2)
将A(2,2)代入目标函数z=3x+2y,
得z=3×2+2×2=6+4=10.
故答案为:10.
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
12.设点P是函数y=-$\sqrt{2x-{x}^{2}}$图象上的任意一点,点P是直线x-2y-6=0上的任意一点,则|PQ|的最小值为.
| A. | $\frac{4}{\sqrt{5}}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{5}$-1 | D. | 以上答案都不对 |