题目内容
已知函数f(x)=x-4+
,x∈(0,4),当x=a时,f(x)取得最小值b,则函数g(x)=a|x+b|的图象为( )
| 9 |
| x+1 |
A、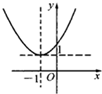 |
B、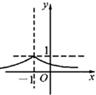 |
C、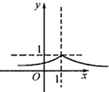 |
D、 |
考点:指数函数的图像变换
专题:函数的性质及应用
分析:先根据基本不等式求出a,b的值,再结合指数函数的性质及函数的图象的平移可求
解答:
解:∵x∈(0,4),
∴x+1>1
∴f(x)=x-4+
=x+1+
-5≥2
-5=1,
当且仅当x=2时取等号,此时函数有最小值1
∴a=2,b=1,
此时g(x)=(
)|x+1|=
,
此函数可以看着函数y=
的图象向左平移1个单位
结合指数函数的图象及选项可知B正确
故选B
∴x+1>1
∴f(x)=x-4+
| 9 |
| x+1 |
| 9 |
| x+1 |
|
当且仅当x=2时取等号,此时函数有最小值1
∴a=2,b=1,
此时g(x)=(
| 1 |
| 2 |
|
此函数可以看着函数y=
|
结合指数函数的图象及选项可知B正确
故选B
点评:本题主要考察了基本不等式在求解函数的最值中的应用,指数函数的图象及函数的平移的应用是解答本题的关键

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设
,
,
为同一平面内具有相同起点的任意三个非零向量,且满足
与
不共线,
⊥
,|
|=|
|,则|
•
|的值一定等于( )
| x1 |
| x2 |
| x3 |
| x1 |
| x2 |
| x1 |
| x3 |
| x1 |
| x3 |
| x2 |
| x3 |
A、以
| ||||
B、以
| ||||
C、以
| ||||
D、以
|
数列{an}的前n项和为Sn=2n2-n+m(m∈R),则“m=0”是“数列{an}为等差数列”的( )
| A、充分必要条件 |
| B、充分而不必要条件 |
| C、必要而不必要条件 |
| D、既不充分也不必要条件 |
下面四个叙述中正确的个数是( )
①∅={0};
②任何一个集合必有两个或两个以上的子集;
③空集没有子集;
④空集是任何一个集合的子集.
①∅={0};
②任何一个集合必有两个或两个以上的子集;
③空集没有子集;
④空集是任何一个集合的子集.
| A、0个 | B、1个 | C、2个 | D、3个 |