题目内容
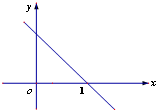函数f（x）的导数f′（x）的图象是如图所示的一条直线l，l与x轴交点坐标为（1，0），则f（0）与f（2）的大小关系为（ ）| A、f（0）＜f（2） |
| B、f（0）＞f（2） |
| C、f（0）=f（2） |
| D、无法确定 |
考点：函数的单调性与导数的关系
专题：导数的概念及应用
分析：根据导函数的图象，写出函数f（x）的单调区间，由导函数图象是一条直线知原函数是二次函数，对称轴是x=1，从而将f（0），f（3）转换到单调区间，就能比较大小了．
解答：
由f′（x）的图象可知：
函数f（x）的增区间为（-∞，1），减区间为（1，+∞），
又导函数f′（x）的图象是一条直线l，
∴原函数是二次项系数小于0的二次函数，其图象的对称轴是x=1．
∴f（x）=f（2-x），
∴f（0）=f（2），
故选C．
函数f（x）的增区间为（-∞，1），减区间为（1，+∞），
又导函数f′（x）的图象是一条直线l，
∴原函数是二次项系数小于0的二次函数，其图象的对称轴是x=1．
∴f（x）=f（2-x），
∴f（0）=f（2），
故选C．
点评：本题考查利用导数研究函数的性质：单调性，进一步比较数的大小，属于一道基础题．
练习册系列答案
相关题目
设a=sin（cos2015°），b=sin（sin2015°），c=cos（sin2015°），d=cos（cos2015°），则（ ）
| A、d＞c＞b＞a |
| B、d＞c＞a＞b |
| C、c＞d＞a＞b |
| D、c＞d＞b＞a |
函数y=sinx-tanx的图象大致是（ ）
A、 |
B、 |
C、 |
D、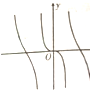 |