题目内容
15.已知函数f(x)=ex,g(x)=ax2-ax.若曲线y=f(x)上存在两点关于直线y=x的对称点在曲线y=g(x)上,则实数a的取值范围是( )| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (0,1)∪(1,+∞) |
分析 利用函数的图形的交点,求出曲线的切线方程,判断切线与曲线有两个交点,推出选项即可.
解答  解:由题意可知(1,0)是曲线y=ax(x-1)与曲线y=lnx的通过公共点,并且当a=1时,两条曲线在(1,0)处的切线都是y=x-1,由导数的定义可知,当0<a<1或a>1时,曲线y=ax(x-1)与直线y=x-1交于两点,也与y=lnx交于两点,
解:由题意可知(1,0)是曲线y=ax(x-1)与曲线y=lnx的通过公共点,并且当a=1时,两条曲线在(1,0)处的切线都是y=x-1,由导数的定义可知,当0<a<1或a>1时,曲线y=ax(x-1)与直线y=x-1交于两点,也与y=lnx交于两点,
故选:D.
点评 本题考查函数的图象的应用,切线方程的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
10.已知两组数据x,y的对应值如下表,若已知x,y是线性相关的且线性回归方程为:$\hat y=\hat bx+\hat a$,经计算知:$\hat b=-1.4$,则$\hat a$=( )
| x | 4 | 5 | 6 | 7 | 8 |
| y | 12 | 10 | 9 | 8 | 6 |
| A. | -0.6 | B. | 0.6 | C. | -17.4 | D. | 17.4 |
13.某种产品的广告费用支出x(万元)与销售额y(万元)之间有如下的对应数据:
(1)请根据上表提供的数据,用最小二乘法求出y关于x 的线性回归方程$\stackrel{∧}{y}$=bx+a
(其中:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$ )求回归直线方程.
(2)据此估计广告费用为12时,销售收入y的值.
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
(2)据此估计广告费用为12时,销售收入y的值.
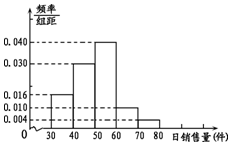 某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.
某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.