题目内容
已知圆C的参数方程为
(θ为参数)在直角坐标系xoy中以O为极点,x轴正半轴为极轴建立极坐标系.已知直线l上两点M,N的极坐标分别为(2,0),(
,
).
(1)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(2)判断直线l与圆C的位置关系.
|
2
| ||
| 3 |
| π |
| 2 |
(1)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(2)判断直线l与圆C的位置关系.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)把圆的参数方程化为直角坐标方程,点M,N的极坐标化为直角坐标,利用中点坐标公式即可得出;
(2)利用点到直线的距离公式求出圆心到直线的距离与半径半径即可得出.
(2)利用点到直线的距离公式求出圆心到直线的距离与半径半径即可得出.
解答:
解:(1)圆C的参数方程
,消去参数θ化为:(x-2)2+(y+
)2=4.
可得圆心C(2,-
),半径r=2.
由直线l上两点M,N的极坐标分别为(2,0),(
,
).
可得直角坐标:(2,0),(0,
).
∴线段MN的中点P(1,
),
∴直线OP的平面直角坐标方程为y=
x.
(2)∵点M、N的坐标为(2,0),(0,
),
∴直线l的方程为x+
y-2=0.
圆心C到此直线的距离d=
=
<2.
∴直线l与圆C相交.
|
| 3 |
可得圆心C(2,-
| 3 |
由直线l上两点M,N的极坐标分别为(2,0),(
2
| ||
| 3 |
| π |
| 2 |
可得直角坐标:(2,0),(0,
2
| ||
| 3 |
∴线段MN的中点P(1,
| ||
| 3 |
∴直线OP的平面直角坐标方程为y=
| ||
| 3 |
(2)∵点M、N的坐标为(2,0),(0,
2
| ||
| 3 |
∴直线l的方程为x+
| 3 |
圆心C到此直线的距离d=
| |2-3-2| | ||
|
| 3 |
| 2 |
∴直线l与圆C相交.
点评:本题考查了把圆的参数方程化为直角坐标方程、极坐标化为直角坐标、中点坐标公式、点到直线的距离公式、直线与圆的位置关系判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知向量
=(a,b),
=(c,d),
=(x,y),定义新运算
*
=(ac+bd,ad+bc),其中等式右边是通常的加法和乘法运算,如果对于任意向量
都有
*
=
成立,那么向量
为( )
| m |
| n |
| p |
| m |
| n |
| m |
| m |
| p |
. |
| m |
| p |
| A、(1,0) |
| B、(-1,0) |
| C、(0,1) |
| D、(0,-1) |
设偶函数f(x)对任意x∈R,都有f(x+3)=-f(x),且当x∈[0,1]时,f(x)=
,则f(5)=( )
| x |
| 5 |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
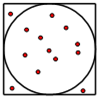 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计出的圆周率π的值为
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在如图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计出的圆周率π的值为