题目内容
已知向量
=(
cos
,cos2
),
=(2sin
,2),设函数f(x)=
•
.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,角A,B,C所对边的长分别为a,b,c,且f(2B-
)=
+1,a=3,b=3
,求sinA的值.
| a |
| 3 |
| x |
| 4 |
| x |
| 4 |
| b |
| x |
| 4 |
| a |
| b |
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)在△ABC中,角A,B,C所对边的长分别为a,b,c,且f(2B-
| π |
| 3 |
| 3 |
| 3 |
考点:三角函数中的恒等变换应用,正弦定理的应用
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)利用向量的数量积公式,结合二倍角、辅助角公式化简函数,即可求函数f(x)的最小正周期;
(Ⅱ)先求出sinB,再利用正弦定理求sinA的值.
(Ⅱ)先求出sinB,再利用正弦定理求sinA的值.
解答:
解:(Ⅰ)∵向量
=(
cos
,cos2
),
=(2sin
,2),函数f(x)=
•
,
∴f(x)=2
cos
2sin
+2cos2
=
sin
+cos
+1=2sin(
+
)+1,
∴T=
=4π;
(Ⅱ)∵f(2B-
)=
+1,
∴2sinB+1=
+1,
∴sinB=
,
∵a=3,b=3
,
∴由正弦定理可得sinA=
=
=
.
| a |
| 3 |
| x |
| 4 |
| x |
| 4 |
| b |
| x |
| 4 |
| a |
| b |
∴f(x)=2
| 3 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 6 |
∴T=
| 2π | ||
|
(Ⅱ)∵f(2B-
| π |
| 3 |
| 3 |
∴2sinB+1=
| 3 |
∴sinB=
| ||
| 2 |
∵a=3,b=3
| 3 |
∴由正弦定理可得sinA=
| asinB |
| b |
3×
| ||||
3
|
| 1 |
| 2 |
点评:本题考查向量的数量积公式,考查三角函数的化简,考查正弦定理的运用,考查学生分析解决问题的能力,正确化简函数是关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
下列四个函数中,以π为最小正周期,且在区间(
,π)上为减函数的是( )
| π |
| 2 |
| A、y=2|sinx| |
| B、y=sin2x |
| C、y=2|cosx| |
| D、y=cos2x |
已知区域M:x2+y2≤4,区域N:-x≤y≤x,随机向区域M中投放一点.该点落在区域N内的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若在区间[0,2]中随机地取两个数,则这两个数中较大的数大于
的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
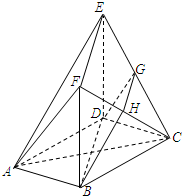 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.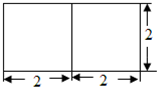 已知一个三棱柱的底面是正三角形、侧棱垂直于底面,其正视图如图所示,则这个三棱柱的体积为
已知一个三棱柱的底面是正三角形、侧棱垂直于底面,其正视图如图所示,则这个三棱柱的体积为