题目内容
规定C
=
,其中x∈R,m是正整数,且C
=1这是组合数C
(n,m是正整数,且m≤n)的一种推广.
(1)C
的值;
(2)组合数的两个性质:C
=C
;C
+C
=C
是否都能推广到C
(x∈R,m∈N*)的情形?若能推广,则写出推广的形式并给予证明,或不能则说明理由;
(3)已知组合数C
是正整数,证明:当x∈Z,m是正整数时,C
∈Z.
m x |
| x(x-1)…(x-m+1) |
| m! |
0 x |
m n |
(1)C
5 -15 |
(2)组合数的两个性质:C
m n |
n-m n |
m n |
m-1 n |
m n+1 |
m x |
(3)已知组合数C
m n |
m x |
考点:组合及组合数公式,进行简单的合情推理
专题:排列组合
分析:(1)根据所给的组合数公式,写出C-155的值,这里与平常所做的题目不同的是组合数的下标是一个负数,在本题的新定义下,按照一般组合数的公式来用.
(2)Cnm=Cnn-m不能推广到Cxm的情形,举出两个反例,Cnm+Cnm-1=Cn+1m能推广到Cxm的情形,可以利用组合数的公式来证明,证明的方法同没有推广之情况相同.
(3)分x≥m,和x<0,根据组合数公式计算即可.
(2)Cnm=Cnn-m不能推广到Cxm的情形,举出两个反例,Cnm+Cnm-1=Cn+1m能推广到Cxm的情形,可以利用组合数的公式来证明,证明的方法同没有推广之情况相同.
(3)分x≥m,和x<0,根据组合数公式计算即可.
解答:
解:(1):(1)C-155=
=-11628;
(2)性质:Cnm=Cnn-m不能推广到Cxm的情形不能推广,例如x=
时,
有定义,但
无意义;
性质:Cnm+Cnm-1=Cn+1m能推广到Cxm的情形,它的推广形式为
+
=
,x∈R,m∈N*,
证明如下:
当m=1时,有
+
=x+1
;
当m≥2时,有
+
=
+
=
(
+1)=
=
(3)当x≥m时,组合数
∈Z;
当x<m时,-x+m-1>0,
∴
=
=(-1)m•
=(-1)m
∈Z.
| -15×(-16)×(-17)×(-18)×(-19) |
| 5! |
(2)性质:Cnm=Cnn-m不能推广到Cxm的情形不能推广,例如x=
| 2 |
| C | 1
|
| C |
|
性质:Cnm+Cnm-1=Cn+1m能推广到Cxm的情形,它的推广形式为
| C | m x |
| C | m-1 x |
| C | m x+1 |
证明如下:
当m=1时,有
| C | 1 x |
| C | 10 x |
| =C | 1 x+1 |
当m≥2时,有
| C | m x |
| C | m-1 x |
| x(x-1)…(x-m+1) |
| m! |
| x(x-1)…(x-m+2) |
| m! |
| x(x-1)(x-m+2) |
| (m-1)! |
| x-m+1 |
| m |
| x(x-1)…(x-m+2)(x+1) |
| m! |
| C | m x+1 |
(3)当x≥m时,组合数
| C | m x |
当x<m时,-x+m-1>0,
∴
| C | m x |
| x(x-1)…(x-m+1) |
| m! |
| (-x+m-1)…(-x+1)(-x) |
| m! |
| C | m -x+m-1 |
点评:本题考查组合数公式,不是在一般的情况下应用组合数公式,而是对于组合数公式推广使用,是一个中档题,题目解起来容易出错.这种题目对于学生帮助不大.

练习册系列答案
相关题目
已知x,y满足
,则z=2x+y的最小值是( )
|
| A、3 | ||
| B、-3 | ||
C、
| ||
| D、0 |
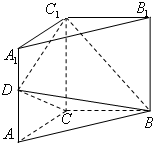 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=