题目内容
1.已知△ABC的三内角A,B,C,所对三边分别为a,b,c,sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,若△ABC的面积S=24,b=10,则a的值是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由题意和两角差的正弦公式化简已知的式子,联立平方关系、内角的范围求出sinA和cosA的值,由条件和三角形的面积公式列出方程求出c,由余弦定理求出a的值.
解答 解:由sin(A-$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$得,$\frac{\sqrt{2}}{2}$(sinA-cosA)=$\frac{\sqrt{2}}{10}$,
则sinA-cosA=$\frac{1}{5}$,联立sin2A+cos2A=1,
解得$\left\{\begin{array}{l}{sinA=\frac{4}{5}}\\{cosA=\frac{3}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{sinA=-\frac{3}{5}}\\{cosA=-\frac{4}{5}}\end{array}\right.$(舍去),
又0<A<π,即sinA=$\frac{4}{5}$,
因为△ABC的面积S=24,b=10,
所以$\frac{1}{2}bcsinA=24$,解得c=6,
由余弦定理得,a2=b2+c2-2bccosA
=100+36-$2×10×6×\frac{3}{5}$=64,
则a=8,
故选D.
点评 本题考查余弦定理,三角形的面积公式,以及两角差的正弦公式等应用,考查化简、计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
4.在等比数列{an}中,已知a7•a19=8,则a3•a23=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
9.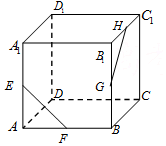 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
16.若函数$f(x)=\frac{2}{3}{x^3}-2{x^2}+ax+10$在区间[-1,4]上单调递减,则实数a的取值范围是( )
| A. | (-∞,-16]∪[2,+∞) | B. | (-16,2) | C. | [2,+∞) | D. | (-∞,-16] |
13.已知△ABC中,A:B:C=1:1:4,则a:b:c等于( )
| A. | 1:1:$\sqrt{3}$ | B. | 2:2:$\sqrt{3}$ | C. | 1:1:2 | D. | 1:1:4 |
10.过抛物线y=ax2(a>0)的焦点F作一直线交抛物线于P,Q两点,若线段PF和线段FQ的长分别是p,q,则$\frac{1}{p}+\frac{1}{q}$等于( )
| A. | $\frac{1}{4a}$ | B. | $\frac{1}{2a}$ | C. | 2a | D. | 4a |