题目内容
18.(Ⅰ) 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段,D为垂足,当P在圆上运动时,求线段PD的中点Q的轨迹方程;(Ⅱ)记(Ⅰ)中的轨迹为曲线为C,斜率为k(k≠0)的直线l交曲线C于M(x1,y1),N(x2,y2)两点,记直线OM,ON的斜率分别为k1,k2,当3(k1+k2)=8k时,证明:直线l过定点.
分析 (Ⅰ)设点Q(x,y),P(x0,y0),则x=x0,y=$\frac{{y}_{0}}{2}$,由x0+y0=4可得x2+4y2=4,即可得答案;
(Ⅱ)依题意可设直线l的方程为x=my+n,代入椭圆方程得:(m2+4)y2+2mny+n2-4=0,利用根与系数的关系、斜率计算公式即可得出结论.
解答 (Ⅰ)解:设点Q(x,y),P(x0,y0),
则x=x0,y=$\frac{{y}_{0}}{2}$.
由x0+y0=4可得x2+4y2=4,即$\frac{{x}^{2}}{4}+{y}^{2}=1$.
∴线段PD的中点Q的轨迹方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)证明:依题意可设直线l的方程为x=my+n,
代入椭圆方程得:(m2+4)y2+2mny+n2-4=0,
则$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=-\frac{2mn}{{m}^{2}+4}}\\{{y}_{1}{y}_{2}=\frac{{n}^{2}-4}{{m}^{2}+4}}\end{array}\right.$,
∴${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}}+\frac{{y}_{2}}{{x}_{2}}$=$\frac{{y}_{1}{x}_{2}+{y}_{2}{x}_{1}}{{x}_{1}{x}_{2}}$=$\frac{{y}_{1}(m{y}_{2}+n)+{y}_{2}(m{y}_{1}+n)}{(m{y}_{1}+n)(m{y}_{2}+n)}$
=$\frac{2m{y}_{1}{y}_{2}+n({y}_{1}+{y}_{2})}{{m}^{2}{y}_{1}{y}_{2}+mn({y}_{1}+{y}_{2})+{n}^{2}}=\frac{2m}{{m}^{2}-{n}^{2}}$,
由条件有$\frac{6m}{{m}^{2}-{n}^{2}}=\frac{8}{m}$,得$n=±\frac{1}{2}m$.
则直线l的方程为$x=my±\frac{1}{2}m$,从而直线l过定点(0,$\frac{1}{2}$)或(0,$-\frac{1}{2}$).
点评 本题考查了轨迹方程,考查了直线与椭圆的位置关系,考查了计算能力,是中档题.

 阅读快车系列答案
阅读快车系列答案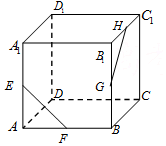 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
| A. | 1:1:$\sqrt{3}$ | B. | 2:2:$\sqrt{3}$ | C. | 1:1:2 | D. | 1:1:4 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{4a}$ | B. | $\frac{1}{2a}$ | C. | 2a | D. | 4a |
| A. | {x|1<x≤2} | B. | {x|1<x<3} | C. | {x|2≤x<3} | D. | {x|1<x<2} |