题目内容
观察如图中各正方形图案,每条边上有n(n≥2)个圆点,第n个图案中圆点的总数是Sn.

按此规律推断出Sn与n的关系式为 .

按此规律推断出Sn与n的关系式为
考点:归纳推理
专题:推理和证明
分析:注意观察前三个图形中圆点的个数可以发现分别为:4,8,12,后一个图形中的圆点个数比前一个图形中圆点多4,所以可得Sn与n的关系式为:S=4n-4.
解答:
解:n=2时,S2=4;n=3时,S3=4+1×4=8;n=4时,S4=4+2×4=12,
∴Sn=4+(n-2)×4=4n-4=4(n-1).
故答案为:4(n-1)
∴Sn=4+(n-2)×4=4n-4=4(n-1).
故答案为:4(n-1)
点评:此题属于规律性问题,解决此类问题,关键在观察、分析已知数据,寻找它们之间的以及与第一个图形的相互联系,探寻其规律.主要培养学生的观察能力和空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数y=f(x)的图象在点(1,f(1))处的切线方程为y=3x-2,则函数g(x)=x2+f(x)的图象在点(1,g(1))处的切线方程为( )
| A、5x-y-3=0 |
| B、5x-y+3=0 |
| C、x-5y+3=0 |
| D、x-5y-3=0 |
与y=x为同一个函数的是( )
A、y=
| |||
B、y=
| |||
C、
| |||
D、y=(
|
sin(
π+x)=( )
| 3 |
| 2 |
| A、sinx | B、cosx |
| C、-sinx | D、-cosx |
i为虚数单位,(1-i)2=( )
| A、-2 i |
| B、2 i |
| C、1-2 i |
| D、2-2 i |
i为虚数单位,则(1+i)(1-i)=( )
| A、2 i |
| B、-2 i |
| C、2 |
| D、-2 |
若圆锥的轴截面是正三角形,则它的侧面积是底面积的( )
| A、4倍 | ||
| B、3倍 | ||
C、
| ||
| D、2倍 |

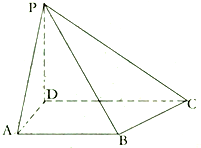 如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=