题目内容
1.在ABC中,角A,B,C所对的边边长分别是a,b,c,若(a2+c2-b2)tanB=$\sqrt{2}$ac.则角B的值为$\frac{π}{4}$或$\frac{3π}{4}$.分析 由余弦定理化简条件得2ac•cosB•tanB=ac,再根据同角三角函数的基本关系得sinB,从而求得角B的值.
解答 解:∵在△ABC中,角A、B、C的对边分别为a、b、c,(a2+c2-b2)tanB=$\sqrt{2}$ac,
∴由余弦定理可得:2ac•cosB•tanB=$\sqrt{2}$ac,
∴sinB=$\frac{\sqrt{2}}{2}$,可得:B=$\frac{π}{4}$ 或 B=$\frac{3π}{4}$,
故答案为:$\frac{π}{4}$ 或 $\frac{3π}{4}$.
点评 本题考查余弦定理的应用,同角三角函数的基本关系,以及根据三角函数值及角的范围求角的大小,属于基础题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
6.在[0,2π]上与-$\frac{π}{7}$终边相同的角是( )
| A. | $\frac{π}{7}$ | B. | $\frac{6π}{7}$ | C. | $\frac{8π}{7}$ | D. | $\frac{13π}{7}$ |
13.点P(x,y)在$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=1+sinθ}\end{array}\right.$(θ为参数)上,则x+y的最大值为( )
| A. | 3+$\sqrt{5}$ | B. | 5+$\sqrt{5}$ | C. | 5 | D. | 6 |
 20名学生某次数学成绩(单位:分)的频率分布直方图如图:
20名学生某次数学成绩(单位:分)的频率分布直方图如图: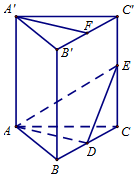 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证: