题目内容
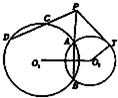 如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点
如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点(1)求证:
| PT |
| PC |
| PD |
| PT |
(2)若⊙O1与⊙O2的半径分别为4,3,其圆心距O1O2=5,PT=
24
| ||
| 5 |
考点:与圆有关的比例线段
专题:选作题,空间位置关系与距离
分析:(1)利用切割线定理,即可证明;
(2)证明∠O1AO2=90°,再利用切割线定理,即可求解.
(2)证明∠O1AO2=90°,再利用切割线定理,即可求解.
解答:
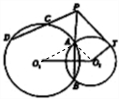 (1)证明:∵PT⊥O2T,
(1)证明:∵PT⊥O2T,
∴PT是⊙O2的切线,
∴PT2=PA•PB,
∵过P的直线交⊙O1于C,D两点
∴PC•PD=PA•PB,
∴PT2=PC•PD,
∴
=
;
(2)解:连接O1A,O2A,
∵⊙O1与⊙O2的半径分别为4,3,其圆心距O1O2=5,
∴O1O22=O1A2+O2A2,
∴∠O1AO2=90°,
设Rt△O1AO2斜边长为h,则h=
=
,AB=2h=
,
∵PT2=PA•PB,PT=
,
∴PA(PA+
)=(
)2,
∴PA=
.
 (1)证明:∵PT⊥O2T,
(1)证明:∵PT⊥O2T,∴PT是⊙O2的切线,
∴PT2=PA•PB,
∵过P的直线交⊙O1于C,D两点
∴PC•PD=PA•PB,
∴PT2=PC•PD,
∴
| PT |
| PC |
| PD |
| PT |
(2)解:连接O1A,O2A,
∵⊙O1与⊙O2的半径分别为4,3,其圆心距O1O2=5,
∴O1O22=O1A2+O2A2,
∴∠O1AO2=90°,
设Rt△O1AO2斜边长为h,则h=
| 3×4 |
| 5 |
| 12 |
| 5 |
| 24 |
| 5 |
∵PT2=PA•PB,PT=
24
| ||
| 5 |
∴PA(PA+
| 24 |
| 5 |
24
| ||
| 5 |
∴PA=
| 24 |
| 5 |
点评:本题考查切割线定理,考查学生分析解决问题的能力,考查学生的计算能力,正确运用切割线定理是关键.

练习册系列答案
相关题目
已知点A、B、C、D均在球O上,AB=BC=
,AC=3,若三棱锥D-ABC体积的最大值为
,则球O的表面积为( )
| 3 |
3
| ||
| 4 |
| A、36π | ||
| B、16π | ||
| C、12π | ||
D、
|
已知a=(log54)2,b=log53,c=ln
,下列结论正确的是( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、c>a>b |
| D、b>a>c |
 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2. 已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=
已知四棱锥P-ABCD,侧面PAD⊥底面ABCD,侧面PAD为等边三角形,底面ABCD为菱形,且∠DAB=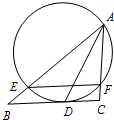 如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.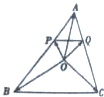 如图,O是△ABC内一点,PQ∥BC,且
如图,O是△ABC内一点,PQ∥BC,且