题目内容
已知函数f(x)=alnx-(a+1)x+
x2(a≥0),若直线l与曲线y=f(x)相切,切点是P(2,0),求直线l的方程.
| 1 |
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:求出函数的导数,求得切线的斜率k,由f(2)=0,可得a=0,可得k=1,由点斜式方程即可得到切线方程.
解答:
解:函数f(x)=alnx-(a+1)x+
x2(a≥0)的导数为f′(x)=
-(a+1)+x,
即有切线的斜率为k=
-a-1+2=
-a+1.
又f(2)=0,即有aln2-2(a+1)+2=0,
解方程得a=0,
故有k=1,
所以直线l的方程为y-0=x-2,
整理得x-y-2=0.
| 1 |
| 2 |
| a |
| x |
即有切线的斜率为k=
| a |
| 2 |
| a |
| 2 |
又f(2)=0,即有aln2-2(a+1)+2=0,
解方程得a=0,
故有k=1,
所以直线l的方程为y-0=x-2,
整理得x-y-2=0.
点评:本题考查导数的运用:求切线方程,主要考查直线方程的求法,正确求导和运用导数的几何意义是解题的关键.

练习册系列答案
相关题目
已知A(2,-4),B(0,6),C(-8,10),则
+2
为( )
| AB |
| BC |
| A、(18,18) |
| B、(-18,18) |
| C、(18,-18) |
| D、(-18,-18) |
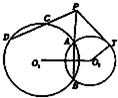 如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点
如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点